cho tam giác abc m thuộc ab n thuộc ac, biết AM/AB = MN/BC. Chứng minh MN//BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Sửa đề: \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(hai góc đồng vị, MN//BC)
\(\widehat{A}\) chung
Do đó: ΔAMN đồng dạng với ΔABC
=>\(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
b: \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
=>\(\dfrac{MN}{8}=\dfrac{2}{5}\)
=>\(MN=2\cdot\dfrac{8}{5}=\dfrac{16}{5}\)

a: Ta có: \(\widehat{MAD}=\widehat{BAD}\)(AD là tia phân giác của góc BAC)
\(\widehat{BAD}=\widehat{MDA}\)(hai góc so le trong, AB//DM)
Do đó: \(\widehat{MAD}=\widehat{MDA}\)
=>ΔMAD cân tại M
b: Xét ΔMND và ΔBDN có
\(\widehat{MND}=\widehat{BDN}\)(hai góc so le trong, NM//BD)
ND chung
\(\widehat{MDN}=\widehat{BND}\)(hai góc so le trong, MD//BN)
Do đó: ΔMND=ΔBDN
c: Ta có: ΔMND=ΔBDN
=>MD=BN
mà MD=MA
nên MA=BN

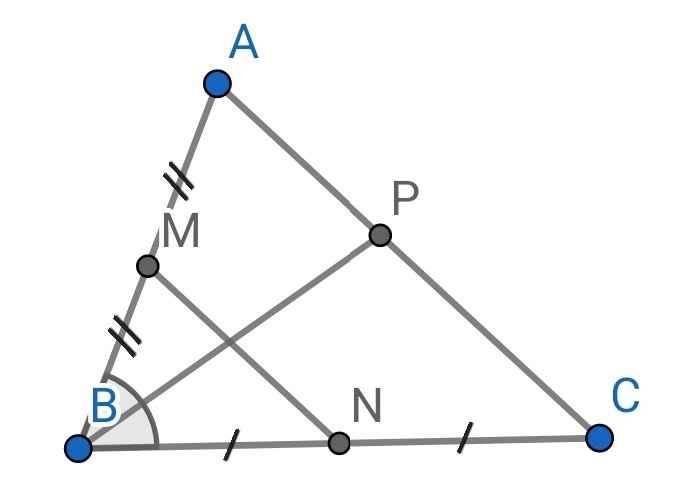 a) Do M là trung điểm của AB (gt)
a) Do M là trung điểm của AB (gt)
⇒ AM = BM = AB : 2 = 6 : 2 = 3 (cm)
Do N là trung điểm của BC (gt)
⇒ BN = CN = BC : 2 = 8 : 2 = 4 (cm)
Ta có:
BM/AM = 3/3 = 1
BN/CN = 4/4 = 1
⇒ BM/AM = BN/CN
⇒ MN // AC (định lý Ta-lét)
b) Ta có:
AM.BC = 3.8 = 24 (cm)
AB.BN = 6.4 = 24 (cm)
⇒ AM.BC = AB.BN
c) Do BP là tia phân giác của ∠ABC (gt)
⇒ BA/BC = PA/PC (1)
Do MN // AC (cmt)
⇒ BA/BC = AM/CN (2)
Từ (1) và (2) ⇒ AM/CN = PA/PC
cho tam giác ABC cân tại A lấy dđiểm M thuộc cạnh AB điểm N thuộc AC sao cho AM=AN chứng minh MN//BC

\(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ACB}=\dfrac{180^o-\widehat{BAC}}{2}\) ( 1)
Mặt khác , ta có AM = AN \(\Rightarrow\Delta AMN\) cân tại A
\(\Rightarrow\widehat{ANM}=\dfrac{180^o-\widehat{MAN}}{2}\) ( mà \(M\in AB;N\in AC\) nên \(\widehat{MAN}=\widehat{BAC}\) )
\(\Rightarrow\widehat{ANM}=\dfrac{180^o-\widehat{BAC}}{2}\) ( 2 )
Từ (1), (2)\(\Rightarrow\) \(\widehat{ACB}=\widehat{ANM}\) mà 2 góc này ở vị trí so le trong tại MN và BC nên MN // BC ( đpcm)
( Giải thích (1) : \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^O\) \(\Rightarrow\widehat{ABC}+\widehat{ACB}=180^O-\widehat{BAC}\) mà \(\widehat{ABC}=\widehat{ACB}\) do \(\Delta ABC\) cân tại A
\(\Rightarrow2.\widehat{ACB}=180^O-\widehat{BAC}\)
\(\Rightarrow\widehat{ACB}=\dfrac{180^O-\widehat{BAC}}{2}\)
Còn (2) thì tương tự như (1) )

a: AC=4cm
b: Xét ΔAMH vuông tại H và ΔAMN vuông tại N có
AM chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔAMN
Suy ra: MH=MN; AH=AN
hay AM là đường trung trực của NH
c: Xét ΔAHN có AH=AN
nên ΔAHN cân tại A
mà \(\widehat{HAN}=60^0\)
nên ΔAHN đều
Ta có : \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\left(gt\right)\Rightarrow\)MN//BC