Giải thật chi tiết giúp vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1
5 tháng 1 2022
Bài 2:
a: Xét ΔBHA vuông tại H và ΔBHD vuông tại H có
BH chung
HA=HD
Do đó: ΔBHA=ΔBHD
b: Ta có: ΔBHA=ΔBHD
nên \(\widehat{ABH}=\widehat{DBH}\)
hay BH là tia phân giác của góc ABD
LM
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
2
10 tháng 11 2021
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
19 tháng 9 2021
\(a,\Leftrightarrow6x^2-15x-6x^2+13x=12\\ \Leftrightarrow-2x=12\Leftrightarrow x=-6\\ b,\Leftrightarrow\left(x-1\right)\left(4x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{4}\end{matrix}\right.\)
HP
19 tháng 9 2021
Bài 2:
a. 8x(5x - 2) - 12(5x - 2) = 0
<=> (8x - 12)(5x - 2) = 0
<=> \(\left[{}\begin{matrix}8x-12=0\\5x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{5}{2}\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
14 tháng 11 2021
Lời giải:
a.
$x(x-7)+2x^2=(x+1)(3x-2)$
$\Leftrightarrow x^2-7x+2x^2=3x^2+x-2$
$\Leftrightarrow 3x^2-7x=3x^2+x-2$
$\Leftrightarrow 2=8x$
$\Leftrightarrow x=\frac{1}{4}$
b.
$(5x-3)(2x+1)-(2x-1)^2+4=0$
$\Leftrightarrow (10x^2-x-3)-(4x^2-4x+1)+4=0$
$\Leftrightarrow 6x^2+3x=0$
$\Leftrightarrow 3x(2x+1)=0$
$\Rightarrow 3x=0$ hoặc $2x+1=0$
$\Leftrightarrow x=0$ hoặc $x=\frac{-1}{2}$
c.
$4x^2-9=(3-2x)(x+2)$
$\Leftrightarrow (2x-3)(2x+3)+(2x-3)(x+2)=0$
$\Leftrightarrow (2x-3)(2x+3+x+2)=0$
$\Leftrightarrow (2x-3)(3x+5)=0$
$\Rightarrow 2x-3=0$ hoặc $3x+5=0$
$\Leftrightarrow x=\frac{3}{2}$ hoặc $x=-\frac{5}{3}$
11 tháng 9 2021
\(2,\\ a,=x^3-8-6x^2+12x=\left(x-2\right)^3\\ b,=25-4x^2+5x+4x^2-25-20x=-15x\\ c,=\left(2x+1\right)^2-\left(2x-1\right)^2\\ =\left(2x+1+2x-1\right)\left(2x+1-2x+1\right)=8x\\ d,=x^3+5x^2+25x+5x^2+25x+125-10x^2-50x-x^3\\ =125\)
3 tháng 10 2021
Bài 2:
a: Ta có: \(x\left(x+3\right)=6x+18\)
\(\Leftrightarrow\left(x+3\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=6\end{matrix}\right.\)
b: Ta có: \(x^2\left(2x+1\right)-x\left(2x+1\right)=0\)
\(\Leftrightarrow x\left(2x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)
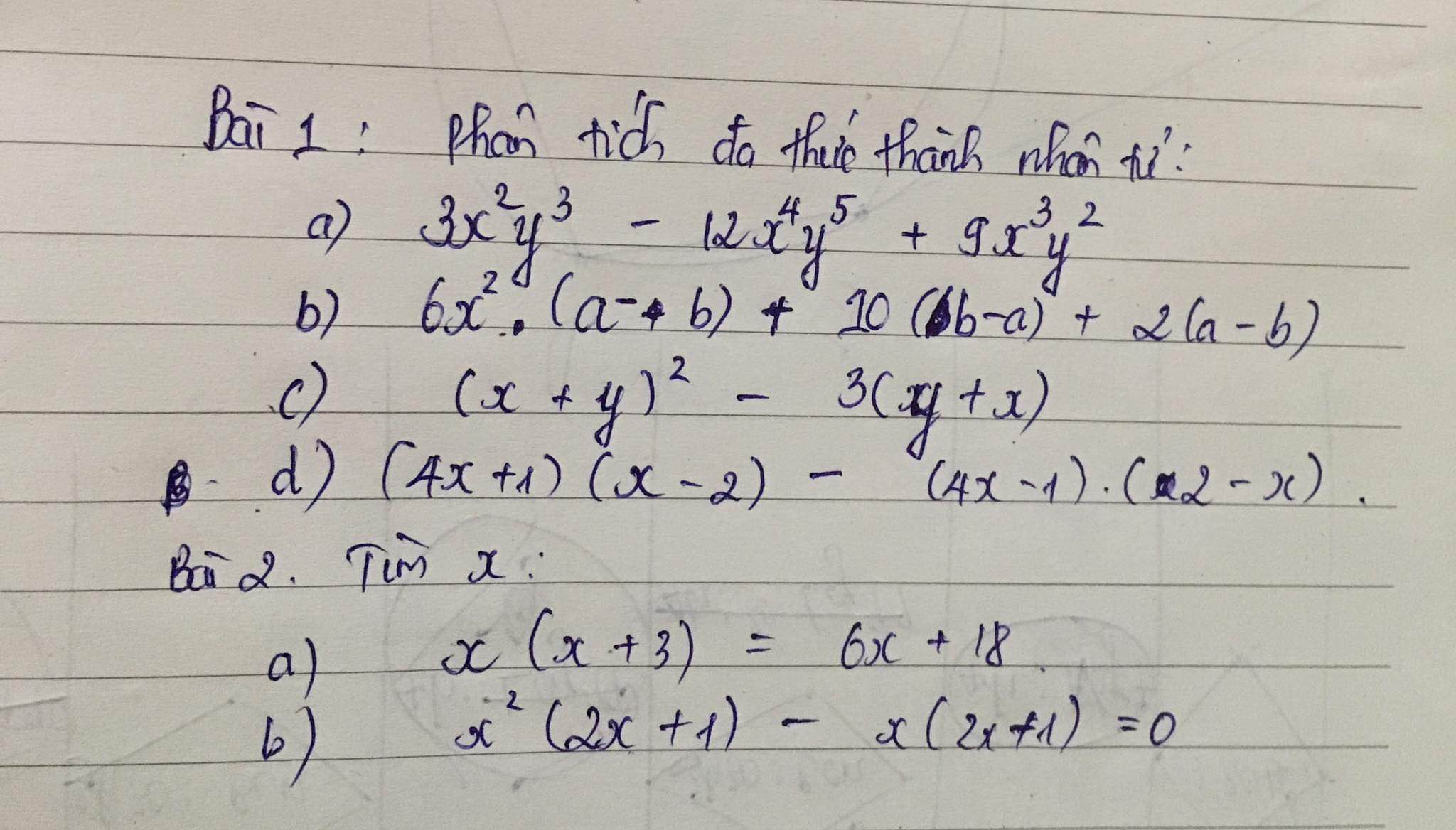
Bài 2:
5x+1=3x
=>5x-3x=-1
=>2x=-1