tỉ số của 2 số là 3/5. hiệu các bình phương của chúng là -64. tìm 2 số đó (nhờ giải ra cho mình nha)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
T
1
NT
1
28 tháng 4 2015
Vì hiệu bình phương của chúng là -64
nên hiệu của chúng là: 8(hoặc -8)
Từ đó xong giải toán hiệu tỉ đó bạn, mà bài này có 2 trường hợp
DP
2
G
18 tháng 4 2016
Vì hiệu bình phương của chúng là -64
nên hiệu cùa chúng là : 8 ( hoặc -8 )
18 tháng 4 2016
Gọi 2 số đó là a và b
Có:
\(\frac{a}{b}=\frac{3}{5}\)
\(\Rightarrow a=\frac{3}{5}b\)
Hiệu hai bình phương của chúng là:
\(a^2-b^2=-64\)
\(\Rightarrow\left(\frac{3}{5}b\right)^2-b^2=-64\)
\(\frac{9}{25}b^2-b^2=-64\)
\(\Rightarrow\frac{-16}{25}b^2=-64\)
\(b^2=100\)
\(\Rightarrow b\in\left\{-10;10\right\}\)
Với b = -10 \(\Rightarrow a=\frac{3}{5}.\left(-10\right)=-6\)
Với b =10 \(\Rightarrow a=\frac{3}{5}.10=6\)
PT
1
CM
11 tháng 5 2019
Gọi hai số phải tìm là a và b (b ≠ 0)
Ta có: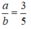 
Đặt a = 3k suy ra b = 5k, do đó:
a2 - b2 = (3k)2 - (5k)2 = 9k2 – 25k2 = -16k2.
Theo đề bài có a2 – b2 = -64, suy ra -16k2 = -64,
suy ra k2 = 4 nên k = 2 hoặc k = -2.
Với k = 2 thì a = 3.2 = 6; b = 5.2 = 10
Với k = -2 thì a = 3.(-2) = -6; b = 5.(-2) = -10
PB
0
13 tháng 7 2017
Gọi hai số cần tìm là a và b \(\left(a\ne0\right)\)
Ta có : \(\dfrac{a}{b}=\dfrac{3}{5}=\dfrac{3k}{5k}\left(k\ne0\right)\)
Vậy \(a=3k , b=5k\) ,do đó :
\(a^2-b^2=\left(3k\right)^2-\left(5k\right)^2=-64\)
\(9k^2-25k^2=-64\)
\(-16k^2=-64\)
\(k^2=4\)
\(k=\pm2.\)
Với \(k=2\) thì \(a=3.1=6,b=5.2=10\)
Với \(k=-2\) thì \(a=3.\left(-2\right)=-6,b=5.\left(-2\right)=-10\)
23 tháng 8 2017
cách làm bạn không phù hợp lớp 6
tham khảo
\(\dfrac{a}{b}=\dfrac{3}{5}\Rightarrow a=\dfrac{3}{5}b\Rightarrow a^2=\dfrac{9}{25}b^2\)
\(a^2-b^2=-64< =>\dfrac{9}{25}b^2-b^2=-64\)
\(b^2\left(\dfrac{9}{25}-1\right)=-64< =>\dfrac{-16}{25}b^2=-64\)
\(\dfrac{b^2}{25}=4=>b^2=100=>\left|b\right|=10\)
\(\left[{}\begin{matrix}b=-10\\b=10\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left(a,b\right)=\left(-6;10\right)\\\left(a,b\right)=\left(6,10\right)\end{matrix}\right.\)