T
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
DD
1
11 tháng 4 2015
Gọi 2 số đó là a và b. Ta có :
\(\frac{a}{b}=\frac{9}{11}\)
Và a2-b2= -146 => a<b. Bạn tự tìm a và b nha !
NT
tỉ số của 2 số là 3/5. hiệu các bình phương của chúng là -64. tìm 2 số đó (nhờ giải ra cho mình nha)
0
NT
1
28 tháng 4 2015
Vì hiệu bình phương của chúng là -64
nên hiệu của chúng là: 8(hoặc -8)
Từ đó xong giải toán hiệu tỉ đó bạn, mà bài này có 2 trường hợp
DP
2
G
18 tháng 4 2016
Vì hiệu bình phương của chúng là -64
nên hiệu cùa chúng là : 8 ( hoặc -8 )
18 tháng 4 2016
Gọi 2 số đó là a và b
Có:
\(\frac{a}{b}=\frac{3}{5}\)
\(\Rightarrow a=\frac{3}{5}b\)
Hiệu hai bình phương của chúng là:
\(a^2-b^2=-64\)
\(\Rightarrow\left(\frac{3}{5}b\right)^2-b^2=-64\)
\(\frac{9}{25}b^2-b^2=-64\)
\(\Rightarrow\frac{-16}{25}b^2=-64\)
\(b^2=100\)
\(\Rightarrow b\in\left\{-10;10\right\}\)
Với b = -10 \(\Rightarrow a=\frac{3}{5}.\left(-10\right)=-6\)
Với b =10 \(\Rightarrow a=\frac{3}{5}.10=6\)
PT
1
CM
11 tháng 5 2019
Gọi hai số phải tìm là a và b (b ≠ 0)
Ta có: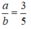 
Đặt a = 3k suy ra b = 5k, do đó:
a2 - b2 = (3k)2 - (5k)2 = 9k2 – 25k2 = -16k2.
Theo đề bài có a2 – b2 = -64, suy ra -16k2 = -64,
suy ra k2 = 4 nên k = 2 hoặc k = -2.
Với k = 2 thì a = 3.2 = 6; b = 5.2 = 10
Với k = -2 thì a = 3.(-2) = -6; b = 5.(-2) = -10
PB
0
13 tháng 7 2017
Gọi hai số cần tìm là a và b \(\left(a\ne0\right)\)
Ta có : \(\dfrac{a}{b}=\dfrac{3}{5}=\dfrac{3k}{5k}\left(k\ne0\right)\)
Vậy \(a=3k , b=5k\) ,do đó :
\(a^2-b^2=\left(3k\right)^2-\left(5k\right)^2=-64\)
\(9k^2-25k^2=-64\)
\(-16k^2=-64\)
\(k^2=4\)
\(k=\pm2.\)
Với \(k=2\) thì \(a=3.1=6,b=5.2=10\)
Với \(k=-2\) thì \(a=3.\left(-2\right)=-6,b=5.\left(-2\right)=-10\)
23 tháng 8 2017
cách làm bạn không phù hợp lớp 6
tham khảo
\(\dfrac{a}{b}=\dfrac{3}{5}\Rightarrow a=\dfrac{3}{5}b\Rightarrow a^2=\dfrac{9}{25}b^2\)
\(a^2-b^2=-64< =>\dfrac{9}{25}b^2-b^2=-64\)
\(b^2\left(\dfrac{9}{25}-1\right)=-64< =>\dfrac{-16}{25}b^2=-64\)
\(\dfrac{b^2}{25}=4=>b^2=100=>\left|b\right|=10\)
\(\left[{}\begin{matrix}b=-10\\b=10\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left(a,b\right)=\left(-6;10\right)\\\left(a,b\right)=\left(6,10\right)\end{matrix}\right.\)
ghi loi giai giup to voi