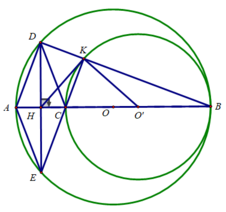
Câu 3: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường
tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D.
Chứng minh AB2 = BD.BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có
\(\widehat{EFA}\) là góc nội tiếp chắn cung EA
\(\widehat{EBA}\) là góc nội tiếp chắn cung EA
Do đó: \(\widehat{EFA}=\widehat{EBA}\)(Hệ quả góc nội tiếp)
hay \(\widehat{MBE}=\widehat{MFA}\)
Xét ΔMBE và ΔMFA có
\(\widehat{MBE}=\widehat{MFA}\)(cmt)
\(\widehat{AMF}\) chung
Do đó: ΔMBE∼ΔMFA(g-g)
Suy ra: \(\dfrac{MB}{MF}=\dfrac{ME}{MA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MA\cdot MB=ME\cdot MF\)(Đpcm)

a) Ta có: OO' = OB – O'B
⇒ Hai đường tròn (O) và (O') tiếp xúc trong tại B

1: góc CHO+góc CNO=180 độ
=>CHON nội tiếp
2: Xét ΔKON và ΔKCH có
góc KON=góc KCH
góc K chung
=>ΔKON đồng dạng với ΔKCH
=>KO/KC=KN/KH
=>KO*KH=KN*KC

a: \(AB=\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
b: Xét ΔOBA vuông tại B có sin OAB=OB/OA=1/2
=>góc OAB=30 độ
=>góc BAC=60 độ
=>ΔBAC đều

2. Để MONP là hình vuông thì đường chéo OM=ON\(\sqrt{2}\)=R\(\sqrt{2}\)
Dựng điểm M: Ta dựng hình vuông OACD, dựng đường tròn tâm O đi qua điểm D, cắt (d) tại M
CM: Từ M vã 2 tiếp tuyến MN và MP ta có: \(MN=\sqrt{MO^2-ON^2}=R\)
Nên tam giác ONM vuông cân tại N. Tương tự tam giác OMP vuông cân tại P do đó MNOP là hình vuông
Bài toán luôn có 2 nghiệm vì \(OM=R\sqrt{2}>R\)
3. Ta có MN và MP là 2 tiếp tuyến của (O) nên MNOP là tứ giác nội tiếp đường tròn đường kính OM. Tâm là trung điểm H của OM. Suy ra tam giác cân MPO nội tiếp trong đường tròn đường kính OM, tâm là H
Kẻ \(OE\perp AB\) thì E là trung điểm của AB (cố định ). kẻ \(HL\perp\left(d\right)\) thì HL//OE nên HL là đường trung bình của tam giác OEM => HL=1/2 OE (không đổi)
Do đó khi M di động trên (d) thì H luôn cách đều (d) một đoạn không đổi, nên H chạy trên đường thẳng (d')//(d) và (d') đi qua trung điểm của đoạn OE
Ta có OM là phân giác góc NMP (tính chất 2 tiếp tuyến cắt nhau). Kẻ tia phân giác góc PNM cắt đường tròn (O) tại điểm F khi đó NF=FP (ứng với góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung bằng nhau)
=> F ở trên OM dó đó F là tâm đường tròn nội tiếp tam giác MNP
Vậy khi M di động trên (d) thì tâm đường tròn nội tiếp tam giác MNP chạy trên đường tròn (O)
AD là tiếp tuyến của (O)
⇒ \(\widehat{DAB}=\widehat{ACB}\) ( cùng chắn \(\stackrel\frown{AB}\) )
AC là tiếp tuyến của (O)
⇒ \(\widehat{CAB}=\widehat{ADB}\) ( cùng chắn \(\stackrel\frown{AB}\) )
⇒ △ CAB ∼ △ ADB ( g - g )
⇒ \(\dfrac{CB}{AB}=\dfrac{AB}{BD}\Rightarrow AB^2=BC.BD\)