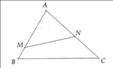
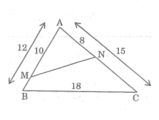
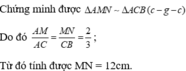trong tam giác ABC biết AB=10cm BC=17cm BD=18cm tính độ dài AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
4 tháng 5 2023
Gọi x là độ dài cạnh AC, Đk: \(x>0\)
Theo bất đẳng thức tam giác, ta có:
\(10-7< x< 10+7\)
\(\leftrightarrow3< x< 17\)
Vì x là một số nguyên tố lớn hơn 11
Nên x = 13
\(\rightarrow\) Chọn D
\(#Hân\)
4 tháng 5 2023
Gọi độ dài của cạnh `AC` là `x (x \ne 0)`
`@` Theo bất đẳng thức trong tam giác, ta có:
`AB+BC > x > AB - BC`
`-> 10+7 > x > 10-7`
`-> 17 > x > 3`
`-> x={16 ; 15 ; 14 ; ... 4}`
Mà `x` là `1` số nguyên tố lớn hơn `11`
`-> x=13 (cm)`
Xét các đáp án trên
`-> D.`
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Ta có:
\(\frac{{AE}}{{AC}} = \frac{{10}}{{15}} = \frac{2}{3};\frac{{AF}}{{AB}} = \frac{8}{{12}} = \frac{2}{3}\)
Xét tam giác \(AFE\) và tam giác \(ABC\) ta có:
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{2}{3}\)
\(\widehat A\) chung
Do đó, \(\Delta AFE\backsim\Delta ABC\) (c.g.c)
Do đó, \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}} = \frac{{EF}}{{BC}} = \frac{2}{3}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Do đó, \(\frac{{EF}}{{BC}} = \frac{2}{3} \Rightarrow EF = \frac{{BC.2}}{3} = \frac{{18.2}}{3} = 12\)
Vậy \(BC = 12cm\).
b) Vì \(FC = FD\) nên tam giác \(FDC\) cân tại \(F\).
Suy ra, \(\widehat {FDC} = \widehat {FCD}\) (tính chất)
Ta có:
\(\frac{{AC}}{{MD}} = \frac{{15}}{{20}} = \frac{3}{4};\frac{{BC}}{{DE}} = \frac{9}{{12}} = \frac{3}{4}\)
Xét tam giác \(ABC\) và tam giác \(MED\) ta có:
\(\frac{{AC}}{{MD}} = \frac{{BC}}{{DE}} = \frac{3}{4}\)
\(\widehat {FCD} = \widehat {FDC}\) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta MED\) (c.g.c).
CM
4 tháng 6 2019
Ta có: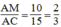 
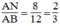
Suy ra: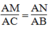 
Xét ΔABC và ΔANM, ta có
+ Góc A chung
+ 
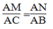
Suy ra:
△
ANM đồng dạng
△
ABC(c.g.c) ⇒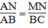 
Vậy MN =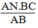 
= (8.18)/12 = 12 cm
NN
9 tháng 11 2018
Do AB// CD=) \(\widehat{ABC}\)=\(\widehat{BC\text{D}}\) (Hai góc so le trong) (*)
Do AB//CD=) \(\widehat{ABC}\)=\(\widehat{B\text{D}C}\) (Hai góc đồng vị) (**)
Từ (*) và (**) =) \(\widehat{BC\text{D}}\)=\(\widehat{B\text{D}C}\)
Mà \(\widehat{CB\text{D}}\)= \(90^0\)
=) Tam giác BCD là tam giác vuông cân tại B
=) BC = BD = 30 cm
Vậy BD = 30 cm
NH
0