lập trình giải và biện luận phương trình bật hai:(m+1)x2-2x+2=0.
với m nhập từ bàn phím
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot\left(m+2\right)\left(3-m\right)\)
\(=\left(2m-2\right)^2+4\left(m+2\right)\left(m-3\right)\)
\(=4m^2-8m+4+4\left(m^2-3m+2m-6\right)\)
\(=4m^2-8m+4+4m^2-4m-24\)
\(=-12m-20\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow-12m-20>0\)
\(\Leftrightarrow-12m>20\)
hay \(m< \dfrac{-5}{3}\)
Để phương trình có nghiệm kép thì Δ=0
\(\Leftrightarrow-12m-20=0\)
\(\Leftrightarrow-12m=20\)
hay \(m=\dfrac{-5}{3}\)
Để phương trình vô nghiệm thì Δ<0
\(\Leftrightarrow-12m-20< 0\)
\(\Leftrightarrow-12m< 20\)
hay \(m>\dfrac{-5}{3}\)
2: ĐKXĐ: \(m\ne-2\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+2}=\dfrac{2m-2}{m+2}\\x_1\cdot x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)
Ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow\dfrac{2m-2}{m+2}=\dfrac{3-m}{m+2}\)
Suy ra: 2m-2=3-m
\(\Leftrightarrow2m+m=3+2\)
\(\Leftrightarrow3m=5\)
hay \(m=\dfrac{5}{3}\)(thỏa ĐK)

Xét m=1 phương trình trở thành \(-4x+1=0\)có nghiệm duy nhất x=-1/4
với m#1 ta có \(\Delta'=\left(m+1\right)^2-m\left(m-1\right)=3m+1\)
với \(\hept{\begin{cases}m\ne1\\m>-\frac{1}{3}\end{cases}}\) pt có hai nghiệm phân biệt
với \(m=-\frac{1}{3}\) pt có nghiệm duy nhất
với \(m< -\frac{1}{3}\)pt vô nghiệm,
theo viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{2\left(m+1\right)}{m-1}=2+\frac{4}{m-1}\\x_1x_2=\frac{m}{m-1}=1+\frac{1}{m-1}\end{cases}}\) lấy phương trình trên trừ đi 4 lần phương trình dưới ta có
\(x_1+x_2-4x_1x_2=-2\)
ý sau, ta có \(\left|x_1-x_2\right|=\frac{2\sqrt{\Delta'}}{\left|a\right|}=\frac{2\sqrt{3m+1}}{\left|m-1\right|}>2\)
\(\frac{\Leftrightarrow4\left(3m+1\right)}{\left(m-1\right)^2}\ge4\Leftrightarrow m^2-5m\le0\Rightarrow m\in\left[0,5\right]\)
kết hợp với đk có 2 nghiệm phân biệt ở câu a , ta có \(m\in\left[0,5\right]\backslash\left\{1\right\}\)

uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else

Tham khảo:
Thuật toán giải phương trình ax + b = 0
- Bằng liệt kê tuần tự
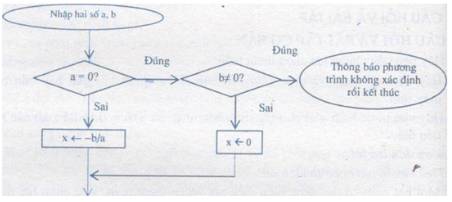
Bước 1: Nhập hai số thực a, b
Bước 2. Nếu a = 0
Bước 2.1. Nếu b ≠0 thì thông báo phương trình vô định, rồi kết thúc;
Bước 2.2. Nếu b = 0 thì gán x
Bước 3: x
Bước 4. Đưa ra nghiệm x, rồi kết thúc.
- Sơ đồ khối:
Đề xuất các test tiêu chuẩn
Để xét tất cả các trường hợp có thể xảy ra, ta sử dụng ba bộ test như sau:
i) a = 0, b = 1 (kiểm tra trường hợp phương trình vô định);
ii) a = 0,b = 0 (kiểm tra trường hợp nghiệm x=0);
iii) a = 3, b = 6 (kiểm tra trường hợp nghiêm , y = -b/a).

1) Với m= 2 PT trở thành x 2 − 4 x + 3 = 0
Giải phương trình tìm được các nghiệm x = 1 ; x = 3.
2) Ta có Δ ' = m 2 − m 2 + 1 = 1 > 0 , ∀ m .
Do đó, phương trình (1) luôn có hai nghiệm phân biệt.
Từ giả thiết ta có x i 2 − 2 m x i + m 2 − 1 = 0 , i = 1 ; 2. x i 3 − 2 m x i 2 + m 2 x i − 2 = x i x i 2 − 2 m x i + m 2 − 1 + x i − 2 = x i − 2 , i = 1 ; 2.
Áp dụng định lí Viét cho phương trình (1) ta có x 1 + x 2 = 2 m ; x 1 . x 2 = m 2 − 1
Ta có
x 1 − 2 + x 2 − 2 = 2 m − 4 ; x 1 − 2 x 2 − 2 = x 1 x 2 − 2 x 1 + x 2 + 4 = m 2 − 1 − 4 m + 4 = m 2 − 4 m + 3
Vậy phương trình bậc hai nhận x 1 3 − 2 m x 1 2 + m 2 x 1 − 2 , x 2 3 − 2 m x 2 2 + m 2 x 2 − 2 là nghiệm là x 2 − 2 m − 4 x + m 2 − 4 m + 3 = 0.

2:
#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
for (i=1; i<=n; i++) if (a[i]%2==0) cout<<a[i]<<" ";
return 0;
}
+) Với \(m=-1\) phương trình trở thành :
\(-2x+2=0\Leftrightarrow x=1\)
+) Với \(m\ne-1\) Ta có :
\(\Delta'=\left(-1\right)^2-2\left(m+1\right)=-2m\)
+ Nếu \(m=0\Leftrightarrow\) pt có 2 nghiệm kép
+ Nếu \(m>0\Leftrightarrow\) pt vô nghiệm
+ Nếu \(m< 0\) pt có 2 nghiệm phân biệt
Vậy...