Cho ΔABC ( ∡A = 900900 ), đường cao AH. Đường tròn đường kính AH cắt các cạnh AB, AC lần lượt tại E và F.a)Chứng minh 4 điểm E, F, C, B cùng thuộc một đường tròn.b)Đường thẳng qua A và vuông góc với E...

ND

Nguyễn Đăng Tuyển

7 tháng 2 2022 - olm

Cho ΔABC ( ∡A = 900900 ), đường cao AH. Đường tròn đường kính AH cắt các cạnh AB, AC lần lượt tại E và F.a)Chứng minh 4 điểm E, F, C, B cùng thuộc một đường tròn.b)Đường thẳng qua A và vuông góc với EF cắt BC tại I. Chứng minh I là trung điểm của BC. c)CM rằng nếu SABCSABC =2. SAEHFSAEHF thì ΔABC vuông...

Đọc tiếp

#Toán lớp 9

1

G

gfffffffh

8 tháng 2 2022

jjjjjjjjjjjjjjjjjjj

Đúng(0)

AL

Anh Lò

28 tháng 2 2023

Câu 5. Cho tam giác ABC vuông tại C (AC < BC), đường cao CH và đường phân giác trong BD (H ∈ AB, De AC). Qua D kẻ đường thẳng vuông góc với AC cắt CH, AB lần lượt tại E và F.a) Chứng minh bốn điểm C, D, H, F cùng thuộc một đường tròn.b) Chứng minh AD.AC =...

Đọc tiếp

#Toán lớp 9

1

AL

Anh Lò

28 tháng 2 2023

hình k co à

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

28 tháng 2 2023

a: Xét tứ giác CDHF có

góc CDF=góc CHF=90 độ

=>CDHF là tứ giác nội tiếp

b: Xét ΔBCA vuông tại C và ΔCDE vuông tại D có

góc CBA=góc DCE

=>ΔBCA đồng dạng với ΔCDE

=>DE/CA=CE/AB

=>DE*AB=CE*CA

BD là phân giác

=>DA/DC=BA/BC

mà CE/CD=BA/BC

nên DA=CE

=>DE*AB=AC*DA

Đúng(0)

LB

Linh Bùi

24 tháng 2 2021

Cho tam giác ABC vuông ở A, đường cao AH. Đường tròn đường kính AH cắt AB, AC lầnlượt ở E, F.a. Chứng minh AEHF là hình chữ nhật.b. Chứng minh BEFC nội tiếp và AE. AB = AF. ACc. Đường thẳng qua A vuông góc với EF cắt BC tại I. CMR: I là trung điểm của BC.d. Chứng minh nếu diện tích tam giác ABC bằng 2 lần diện tích của tứ giác AEHF thì tam giác ABCvuông cân.Mình lm đc câu a,b r giúp mình câu c,d...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

24 tháng 2 2021

a) Xét (O) có

ΔAFH nội tiếp đường tròn(A,F,H\(\in\)(O))

AH là đường kính(gt)

Do đó: ΔAFH vuông tại F(Định lí)

Xét (O) có

ΔAEH nội tiếp đường tròn(A,E,H\(\in\)(O))

Do đó: ΔAEH vuông tại E(Định lí)

Xét tứ giác AEHF có

\(\widehat{FAE}=90^0\left(\widehat{BAC}=90^0\right)\)

\(\widehat{AEH}=90^0\)(ΔAEH vuông tại E)

\(\widehat{AFH}=90^0\)(ΔAHF vuông tại F)

Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

Đúng(2)

OL

OTP là thật t là giả

17 tháng 7 2023

Cho tam giác ABC nhọn (AB < AC) , vẽ đường tròn tâm O đường kính BC cắt AB và AC tại D và E, CD cắt BE tại H. a) Chứng minh AH vuông góc BC. b) Chứng minh 4 điểm A, E, H, D cùng thuộc một đường đường tròn, xác định tâm I của đường tròn qua 4 điểm. c) Chứng minh 4 điểm B, C, D, E cùng thuộc 1 đường tròn. Xác định tâm O của đường tròn đi qua 4 điểm d) Chứng minh OI vuông góc với DE

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

23 tháng 7 2023

a:

góc BDC=góc BEC=1/2*sđ cung BC=90 độ

=>CD vuông góc AB và BE vuông góc AC

Xét ΔABC có

CD,BE là đường cao

CD cắt BE tại H

=>H là trực tâm

=>AH vuông góc BC

b: góc AEH+góc ADH=180 độ

=>AEHD nội tiếp đường tròn đường kính AH

=>I là trung điểm của AH

c: góc BDC=góc BEC=90 độ

=>BDEC nội tiếp đường tròn đường kính BC

=>O là trung điểm của BC

d: ID=IE

OD=OE

=>OI là trung trực của DE

=>OI vuông góc DE

Đúng(0)

BT

Bùi Tuấn Trung

4 tháng 9 2023

Cho tam giác ABC nhọn. Đường tròn đường kính AB cắt các cạnh AC, BC lần lượt tại điểm D và E. Gọi H là giao điểm của AE và BD. Chứng minh rằng: a) Bốn điểm C, D, H, E cùng thuộc 1 đường tròn. b) CH vuông góc với AB. c) \(AH\cdot AE+BH\cdot...

Đọc tiếp

#Toán lớp 9

3

NL

Nguyễn Lê Phước Thịnh

4 tháng 9 2023

a:

Gọi O là trung điểm của AB

Xét (O) có

ΔADB nội tiếp

AB là đường kính

Do đó: ΔADB vuông tại D

=>BD vuông góc AC tại D

Xét (O) có

ΔAEB nội tiếp

AB là đường kính

Do đó: ΔAEB vuông tại E

=>AE vuông góc BC tại E

Xét tứ giác CDHE có

góc CDH+góc CEH=180 độ

=>CDHE nội tiếp

b: Xét ΔCAB có

AE,BD là đường cao

AE cắt BD tại H

=>H là trực tâm

=>CH vuông góc AB tại K

c: Xét ΔAKH vuông tại K và ΔAEB vuông tại E có

góc KAH chung

Do đó: ΔAKH đồng dạng với ΔAEB

=>AK/AE=AH/AB

=>AH*AE=AK*AB

Xét ΔBKH vuông tại K và ΔBDA vuông tại D có

góc KBH chung

Do đó: ΔBKH đồng dạng với ΔBDA
=>BK/BD=BH/BA

=>BK*BA=BH*BD

AH*AE+BH*BD

=AK*AB+BK*BA

=BA^2

Đúng(1)

JW

Jackson Williams

4 tháng 9 2023

a) ....................... =) C, D, H, E cùng thuộc 1 đường tròn.

b) ....................... =) CH ⊥ AB.

c) ....................... =) AH.AE + BH.BD = AB².

Đúng(0)

NV

Nguyen van quan

5 tháng 9 2023

cho tam giác abc nhọn ( ab < ac) . vẽ đường tròn tâm o đường kính bc cắt ab và ac tại f và e , cf cắt be tại h
a) chứng minh ah vuông góc với bc tại d
b) chứng minh 4 điểm a,f,h,e cùng thuộc 1 đường tròn , xác định tâm i của đường tròn này
c) chứng minh ie và if là 2 tiếp tuyến của (o)

#Toán lớp 9

2

NV

Nguyen van quan

5 tháng 9 2023

giúp mik với các bạn

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

5 tháng 9 2023

a: Xét (O) có

ΔBFC nội tiếp

BC là đường kính

Do đó: ΔBFC vuông tại F

=>CF vuông góc AB

Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>BE vuông góc AC

Xét ΔABC có

BE,CF là đường cao

BE cắt CF tại H

Do đó: H là trực tâm

=>AH vuông góc BC tại D

b: Xét tứ giác AFHE có

góc AFH+góc AEH=90+90=180 độ

=>AFHE nội tiếp đường tròn đường kính AH

I là trung điẻm của AH

c:

Xét tứ giác BFHD có

góc BFH+góc BDH=180 độ

=>BFHD nội tiếp

=>góc DFH=góc DBH=góc EBC

góc IFD=góc IFH+góc DFH

=góc IHF+góc EBC

=góc DHC+góc EBC

=90 độ-góc FCB+góc EBC

=90 độ

=>IF là tiếp tuyến của (O)

Xét ΔIFD và ΔIED có

IF=IE

FD=ED

ID chung

=>ΔIFD=ΔIED

=>góc IED=góc IFD=90 độ

=>IE là tiếp tuyến của (O)

Đúng(1)

HT

Hoang Tran

25 tháng 7 2021

Cho đường tròn tâm O, đường kính BC. A thuộc đường tròn tâm O. AH vuông góc BC. Đường tròn đường kính AH cắt AB, AC và cắt đường tròn tâm O tại E, F, K.

a) Chứng minh: AO vuông góc EF.

b) AK cắt BC tại T. Chứng minh: T, E, F thẳng hàng.

Mọi người giúp em với ạ em cần gấp

#Toán lớp 9

3

AT

An Thy

25 tháng 7 2021

a) Vì AH là đường kính \(\Rightarrow\angle AEH=\angle AFH=90\)

Vì BC là đường kính \(\Rightarrow\angle BAC=90\Rightarrow\angle AEH=\angle AFH=\angle EAF=90\)

\(\Rightarrow AEHF\) là hình chữ nhật

\(\Rightarrow\angle AEF=\angle AHF=\angle ACH\left(=90-\angle HAC\right)\)

\(\Rightarrow\angle AEF+\angle ABC=\angle ACH+\angle ABC=90\)

mà \(\angle ABC=\angle BAO\) (\(\Delta ABO\) cân tại O)

\(\Rightarrow\angle AEF+\angle BAO=90\Rightarrow EF\bot AO\)

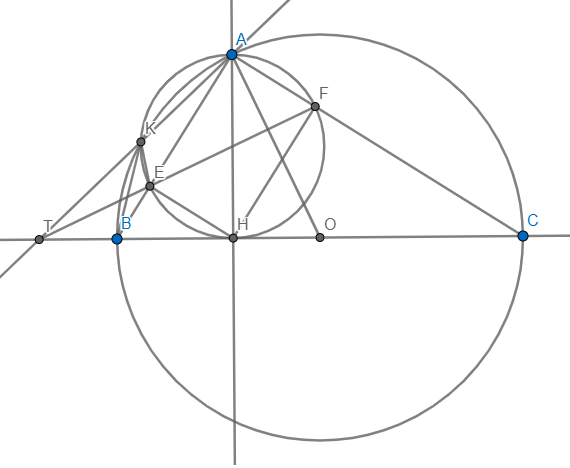
c) EF cắt BC tại T'.T'A cắt (O) tại K'

Vì \(\angle AEF=\angle ACH\Rightarrow EFCB\) nội tiếp

Xét \(\Delta T'EB\) và \(\Delta T'CF:\) Ta có: \(\left\{{}\begin{matrix}\angle T'EB=\angle T'CF\\\angle FT'Cchung\end{matrix}\right.\)

\(\Rightarrow\Delta T'EB\sim\Delta T'CF\left(g-g\right)\Rightarrow\dfrac{T'E}{T'C}=\dfrac{T'B}{T'F}\Rightarrow T'E.T'F=T'B.T'C\)

Vì AK'BC nội tiếp \(\Rightarrow\angle T'K'B=\angle T'CA\)

Xét \(\Delta T'K'B\) và \(\Delta T'CA:\) Ta có: \(\left\{{}\begin{matrix}\angle T'K'B=\angle T'CA\\\angle AT'Cchung\end{matrix}\right.\)

\(\Rightarrow\Delta T'K'B\sim\Delta T'CA\left(g-g\right)\Rightarrow\dfrac{T'K'}{T'C}=\dfrac{T'B}{T'A}\Rightarrow T'K'.T'A=T'B.T'C\)

\(\Rightarrow T'K'.T'A=T'E.T'F\Rightarrow\dfrac{T'K'}{T'F}=\dfrac{T'E}{T'A}\)

Xét \(\Delta T'EK'\) và \(\Delta T'AF:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{T'K'}{T'F}=\dfrac{T'E}{T'A}\\\angle FT'Achung\end{matrix}\right.\)

\(\Rightarrow\Delta T'EK'\sim\Delta T'AF\left(c-g-c\right)\Rightarrow\angle T'K'E=\angle T'FA\)

\(\Rightarrow AK'EF\) nội tiếp \(\Rightarrow K'\in\) đường tròn đường kính AH

\(\Rightarrow K'\equiv K\Rightarrow T'\equiv T\Rightarrow T,E,F\) thẳng hàng

undefined

Đúng(1)

HT

Hoang Tran

25 tháng 7 2021

undefined

Đúng(0)

NV

Nguyễn Việt

5 tháng 6 2016 - olm

Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm O đường kính AH, đường tròn này cắt AB, AC lần lượt tại E và F. Gọi K là trung điểm của HC, đường vuông góc với EC tại C cắt FK tại P. Chứng minh rằng: BP song song với AC

#Toán lớp 9

0

D

dttnhu

26 tháng 10 2023

Cho tam giác ABC nhọn vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và F. BF cắt CE tại H. a) cm AH vuông góc với BC; b) cm AE.AB = AF.AC c) Cm góc AEF = góc ACB ; d) Cm 4 điểm A, E, H, F cùng thuộc 1 đường tròn

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

26 tháng 10 2023

a: Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>CE\(\perp\)AB

Xét (O) có

ΔBFC nội tiếp

BC là đường kính

Do đó: ΔBFC vuông tại F

=>BF\(\perp\)AC

XétΔABC có

CE,BF là đường cao

CE cắt BF tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC

b: Xét ΔAEC vuông tại E và ΔAFB vuông tại F có

\(\widehat{A}\) chung

Do đó: ΔAEC ~ΔAFB

=>\(\dfrac{AE}{AF}=\dfrac{AC}{AB}\)

=>\(AE\cdot AB=AC\cdot AF;\dfrac{AE}{AC}=\dfrac{AF}{AB}\)

c: Xét ΔAEF và ΔACB có

\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)

\(\widehat{FAE}\) chung

Do đó: ΔAEF~ΔACB

=>\(\widehat{AEF}=\widehat{ACB}\)

d: Xét tứ giác AEHF có

\(\widehat{AEH}+\widehat{AFH}=180^0\)

=>AEHF là tứ giác nội tiếp

=>A,E,H,F cùng thuộc một đường tròn

Đúng(1)

HT

Huỳnh Trần Thảo Nguyên

3 tháng 12 2018 - olm

Cho tam giác ABC nội tiếp đường tròn (O) đường kính BC. Kẻ đường cao AH của tam giác ABC. Biết BC=20cm, AH/AC= 3/4

1. Tính AB và AC

2. Đường tròn đường kính AH cắt (O), AB, AC lần lượt tại M,D,E. DE cắt BC tại K. Chứng minh: A,M,K thẳng hàng

3. Chứng minh: B, D, E, C cùng thuộc một đường tròn

#Toán lớp 9

0

C

Chan

27 tháng 12 2020

cho ΔABC vuông tại A, có đường cao AH. Gọi K là trung điểm AH. Từ H hạ vuông góc với AB và AC tại D và E. Đường tròn (K;AK) cắt đường tròn (O) đường kính BC tại I, AI cắt BC tại M. Chứng minh:

a) 5 điểm A,I,D,H,E thẳng hàng

b) MK ⊥ AO

c) 4 điểm M,D,K,E thẳng hàng

d) MD.ME=MH²

#Toán lớp 9

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP