 .giúp ming với
.giúp ming với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}=\frac{1}{2.2}+\frac{1}{3.3}+\frac{1}{4.4}+...+\frac{1}{100.100}\)
\(< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{99.100}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=1-\frac{1}{100}< 1\)(ĐPCM)

Do n không chia hết cho 3 => n chia 3 dư 1 hoặc 2
+ Nếu n chia 3 dư 1 thì n = 3.k + 1 => n2 = (3.k + 1).(3.k + 1)
= (3.k + 1).3.k + (3.k + 1)
= 9.k2 + 3.k + 3.k + 1 chia 3 dư 1
+ Nếu n chia 3 dư 2 thì n = 3k + 2 => n2 = (3.k + 2).(3.k + 2)
= (3.k + 2).3.k + (3.k + 2).2
= 9.k2 + 6.k + 6.k + 4 chia 3 dư 1
=> n2 luôn chia 3 dư 1 với n không chia hết cho 3 (đpcm)

16, \(5\sqrt{3}:\sqrt{15}\)
\(=5\sqrt{3}:\sqrt{5}\cdot\sqrt{3}\)
\(=\dfrac{5\sqrt{3}}{\sqrt{5}\cdot\sqrt{3}}\)
\(=\dfrac{5}{\sqrt{5}}\)
\(=\dfrac{\sqrt{5}\cdot\sqrt{5}}{\sqrt{5}}\)
\(=\sqrt{5}\)

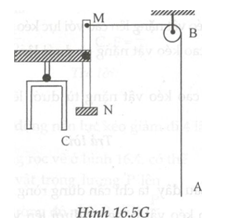
Có thể thiết kế phương án như hình vẽ (H.16.5G ) Hệ thống chuông chỉ gồm 1 ròng rọc B và đòn bẩy MN. Khi kéo dây AB đòn bẩy gắn búa ở N sẽ đánh vào chuông C.

Ta có :
2017 - p2 = 2016 - ( p2 - 1 )
Lại có : p2 - 1 = p2 + p - p - 1 = ( p2 + p ) - ( p + 1 ) = p . ( p + 1 ) - ( p + 1 ) = ( p - 1 ) ( p + 1 )
Vì p là số nguyên tố lớn hơn 3 \(\Rightarrow\)p là số lẻ \(\Rightarrow\)p - 1 và p + 1 là hai số chẵn liên tiếp \(\Rightarrow\)( p - 1 ) ( p + 1 ) \(⋮\)8 ( 1 )
p có dạng 3k + 1 hoặc 3k + 2
nếu p = 3k + 1 thì ( p - 1 ) ( p + 1 ) = ( 3k + 1 - 1 ) ( 3k + 1 + 1 ) = 3k . ( 3k + 2 ) \(⋮\)3
nếu p = 3k + 2 thì ( p - 1 ) ( p + 1 ) = ( 3k + 2 - 1 ) ( 3k + 2 + 1 ) = ( 3k + 1 ) . 3 . ( k + 1 ) \(⋮\)3
\(\Rightarrow\)( p - 1 ) ( p + 1 ) \(⋮\)3 ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\)( p - 1 ) ( p + 1 ) \(⋮\)3 , 8 hay p2 - 1 \(⋮\)3,8
Mà ( 3 ; 8 ) = 1 \(\Rightarrow\)p2 - 1 \(⋮\)24
Mà 2016 \(⋮\)24
\(\Rightarrow\)2016 - ( p2 - 1 ) \(⋮\)24 hay 2017 - p2 \(⋮\) 24
Vậy 2017 - p2 \(⋮\)24

1. go - went
2. come - came
3. buy - bought
4. have - had
câu 5 mik chưa biết
1.Go->went
2.Come->came
3.Buy->bought
4.Have->had
5.Do->did