Bóng của ánh nắng mặt trời chiếu tới cây cách cây một khoảng 20 (m) và tạo với phương nằm ngang một góc 30 độ. Tính chiều cao của cây.
Giup mình với ạ!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
16 tháng 7 2017
1) Hình vẽ:
a) Khi gậy đặt thẳng đứng, bóng của gậy có chiều dài:
b) Để bóng cây gậy dài nhất, gậy phải được đặt theo phương vuông góc với phương truyền sáng. Þ Góc tạo bởi cây gậy và phương ngang là 300.
Chiều dài lớn nhất của bóng: 
.
2) Hình vẽ minh họa:
Do tia phản xạ có phương nằm ngang nên 
.(so le trong) 
TH1, hình 2c: 
TH2, hình 2b: 
Từ hình vẽ: 
14 tháng 7 2023
7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)
25 tháng 10 2021
Gọi C là điểm đặt mắt người đó, BE là chiều cao của cây và CF là chiều cao người đó
Xét tứ giác AECF có:
\(\widehat{A}=\widehat{E}=\widehat{F}=90^0\)
=> AECF là hình chữ nhật
=> \(AE=CF=1,7m;AC=EF=30m\)
Áp dụng tslg trong tam giác ABC:
\(tanC=\dfrac{AB}{AC}\Rightarrow AB=30.tan35^0\approx21\left(m\right)\)
Chiều cao của cây: \(BE=AB+AE\approx21+1,7\approx23\left(m\right)\)
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
Theo hình vẽ ta có:
$BC=DE=1,7$ (m)
$AB=BE.\tan \widehat{AEB}=30.\tan 35^0=21$ (m)
Chiều cao của cây là:
$AC=AB+BC=21+1,7=22,7$ (m)
VT
22 tháng 3 2019
Đáp án C
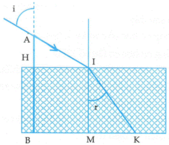
Bóng của cây cọc là B K = B M + M K
Với
Theo định luật khúc xạ tại I
Mặt khác
Vậy bóng của cây cọc trên mặt nước là:
Gọi chiều cao cây là AB
bóng ánh nắng chiếu tới cây là BC ( AB;BC > 0 )
Theo bài ra : Xét tam giác ABC
cho mình bổ sung thêm nhé :
Xét tam giác ABC vuông tại A
ta có : tan^ACB = AB/BC = \(\dfrac{\sqrt{3}}{3}=\dfrac{AB}{20}\Rightarrow AB=\dfrac{20\sqrt{3}}{3}m\)