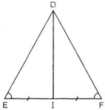
Cho tam giác DEF cân tại D với đường trung tuyến DI a) Chứng minh: Tam giác DEI= Tam giác DFI b) Các góc DIE và góc DIF là hững góc gì? c) Biết DI= 12cm, EF= 10cm. Hãy tính độ dài cạnh DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn tham khỏa đường link này nha /hoi-dap/detail/220486054053.html

a) Chứng minh △ DEF= △ DIF
+ Vì △ DEF cân tại D(gt)
\(\Rightarrow\) DE=DF và góc DEF= góc DFE
+ Vì DI là trung tuyến(gt)
\(\Rightarrow\)DI là đg cao hay DI ⊥ EF
+Xét △ DEI và △ DFI có
DE=DF(cmt)
IE=IF( do I là trung điểm- DI là trung tuyến)
góc DEF= góc DFE(cmt)
⇒ △ DEF= △ DFI( c-g-c)
b) Chứng minh DI ⊥ EF
+Vì △ DEF= △ DFI (cmt)
\(\Rightarrow\) góc EID= góc FID
mà góc EID + góc FID= 180 độ
\(\rightarrow\) góc EID= FID= 90 độ
Vậy DI ⊥ EF(đpcm)
a) Tam giác DEF cân có DE= DF , DI là trung tuyến đồng thời là đường cao,
Xét Tam giác DEI và Tam giác DFI có: DE=DF, góc DEF= góc DFE( tam giác DEF cân), EI= IF
Tam giác DEI = Tam giác DFI (cgc)
b) từ câu a ta có góc EID= FID (góc tương ứng)
Mà EID+ FID = 180 ----> EID= FID =900
DI vuông góc EF.
![]() Học tốt nha!
Học tốt nha!

a: Xét ΔDEI và ΔDFI có
DE=DF
EI=FI
DI chung
=>ΔDEI=ΔDFI
b: ΔDEF cân tại D
mà DI là trung tuyến
nên DI vuông góc EF
c: Xét ΔDFE có FI/FE=FN/FD
nên IN//ED

a)tam giác dei=tg dfi (c.c.c)
b)nên góc dif bằng góc die bằng 90 độ nên di vuông góc với ef
c)EN là đường trung tuyến. nên nd=nf nên in là đường trung tuyến của tam giác vuông dif
trên tia đối tia ini vẽ điểm m sao cho nm=ni
chứng minh được tam giác dni=tam giác fnm (c.g.c)
nên di=ef (2ctu);và góc din bằng góc nmf(mà 2 góc này ở vị trí so le trong )nên di song song với mf nên goc dif bằng góc mfi bằng 90 độ
chứng minh đc tam giác dif =tam giác mfi (c.g.c) nên cạnh df =im nên in=1/2df nên in=nf nên tam giác inf cân tai n nên góc nif bằng nfi mà nfi = góc dei (tam giác def cân tại d) nên góc nif bằng góc dei
mà 2 góc này ở vị trí đồng vị nên in song song với de
bạn ơi ,bạn tự vẽ hình đi nha


Xét ΔDEI và ΔDFI có:
DI là cạnh chung
DE = DF (gt)
IE = IF (I là trung điểm EF)
⇒ ΔDEI = ΔDFI (c.c.c)

chắc câu a và b bạn đả giải dc nên mình chỉ trinh bày câu c
bạn tự vẽ hình nha
c)en là đường trung tuyến của tam giác def nên nd=nf suy ra in là đường trung tuyến của tam giác dif
trên tia đối của tia ni , vẽ diểm t sao cho nt=ni
cmđ:tam giac dni=fnt(c.g.c)
suy ra di =tf(2ctu)và góc din=ftn mà 2 góc này ở vị trí so le trong nên di song song với tf suy ra góc die=tfi =90 độ
cmđ tam giác dif =tfi (c.g.c) suy ra df =ti (2 cạnh tương ứng) suy ra df/2=ti/2 nên dn=nf=ni=nt
ni=nf suy ra tam giác inf cân tại n nên góc nif =nfi mà dfi =dei (tam giác def cân tại d) nên góc nif=dei
và :2 góc này ở vị trí đồng vị
nên in song song với de

a) Xét ΔDEI và ΔDFI có
DE=DF(ΔDEF cân tại D)
DI chung
EI=FI(I là trung điểm của EF)
Do đó: ΔDEI=ΔDFI(c-c-c)
b) Ta có: I là trung điểm của EF(gt)
nên \(IE=IF=\dfrac{EF}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Ta có: ΔDEI=ΔDFI(cmt)
nên \(\widehat{DIE}=\widehat{DIF}\)(hai góc tương ứng)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)
nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)
Áp dụng định lí Pytago vào ΔDEI vuông tại I, ta được:
\(DE^2=DI^2+IE^2\)
\(\Leftrightarrow DE^2=5^2+12^2=169\)
hay DE=13(cm)

a) Xét ΔDEI và ΔDFI có
DE=DF(ΔDEF cân tại D)
DI chung
EI=FI(I là trung điểm của EF)
Do đó: ΔDEI=ΔDFI(c-c-c)
b) Ta có: ΔDEI=ΔDFI(cmt)
nên \(\widehat{DIE}=\widehat{DIF}\)(hai góc tương ứng)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)
nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)
Vậy: Các góc DIE và DIF là các góc vuông)