Lm giúp em bài này với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
góc B chung
Do đó: ΔAHB\(\sim\)ΔCAB
Suy ra: BA/BC=BH/BA
hay \(BA^2=BH\cdot BC\)
b: \(AC=\sqrt{BC^2-AB^2}=24\left(cm\right)\)
\(HC=\dfrac{AC^2}{BC}=\dfrac{24^2}{40}=14.4\left(cm\right)\)



Bài 3:
a: Ta có: \(x-2\sqrt{x+8}=0\)
\(\Leftrightarrow\sqrt{4x+32}=x\)
\(\Leftrightarrow4x+32=x^2\)
\(\Leftrightarrow x^2-4x-32=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\left(nhận\right)\\x=-4\left(loại\right)\end{matrix}\right.\)
b: Ta có: \(3\sqrt{x+5}=4x-7\)
\(\Leftrightarrow\left(4x-7\right)^2=9x+45\)
\(\Leftrightarrow16x^2-56x+49-9x-45=0\)
\(\Leftrightarrow16x^2-65x+4=0\)
\(\Leftrightarrow16x^2-64x-x+4=0\)
\(\Leftrightarrow\left(x-4\right)\left(16x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{16}\end{matrix}\right.\)

Bài 1:
Gọi chiều dài là x(Điều kiện: x>10,5)
Chiều rộng là 21-x
Theo đề, ta có: \(x^2+\left(21-x\right)^2=225\)
\(\Leftrightarrow x^2+x^2-42x+441-225=0\)
\(\Leftrightarrow2x^2-42x+216=0\)
\(\Leftrightarrow x^2-21x+108=0\)
\(\Leftrightarrow\left(x-12\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=12\left(nhận\right)\\x=9\left(loại\right)\end{matrix}\right.\)
vậy: Chiều dài là 12m
Chiều rộng là 9m

đặt M là n^3 -9n^2+2n.
TH1 : n có dạng 2k => M chia hết cho 2 (bạn tự cm)
TH2 ; n có dạng 2k+1 => M = (2k+1)^3-9(2k+1)^2+2n
=8k^3+6k+12k^2+1-9(4k^2+4k+1)+2n = ... => M chia hết cho 2 với mọi n (1)
Xét n có dạng 3k => M chia hết cho 3
Xét n có dạng 3k+1 => n^3+2n=(3k+1)^3+2(3k+1)=27k^3+9k+27k^2+6k+3 chia hết cho 3 mà 9n^2 cũng chia hết cho 3 => M chia hết cho 3
Tương tự bạn xét n =3k+2....
=> M chia hết cho 3 vs mọi n (2)
Từ (1) và (2) => M chia hết cho 6

Lời giải:
Nếu $x+y+z+t=0$ thì $M=\frac{-t}{t}=\frac{-x}{x}=\frac{-z}{z}=-1$
$\Rightarrow (M-1)^{2025}=(-1-1)^{2025}=(-2)^{2025}$
Nếu $x+y+z+t\neq 0$. Áp dụng TCDTSBN:
$M=\frac{x+y+z}{t}=\frac{y+z+t}{x}=\frac{z+t+x}{y}=\frac{t+x+y}{z}=\frac{x+y+z+y+z+t+z+t+x+t+x+y}{t+x+y+z}=\frac{3(x+y+z+t)}{x+y+z+t}=3$
$\Rightarrow (M-1)^{2025}=2^{2025}$


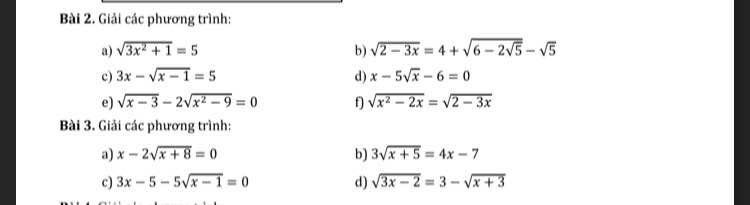

1:
#include <bits/stdc++.h>
using namespace std;
long long x,i,n,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x%2==0) t=t+x;
}
cout<<t;
return 0;
}
2:
#include <bits/stdc++.h>
using namespace std;
long long x,n,i,dem;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x<0) dem++;
}
cout<<dem;
return 0;
}
Cảm ơn ạ