giúp mình giải HPT này với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
Chắc là biến đổi trong bài tìm pt mặt phẳng
Từ hệ 2 pt đầu ta rút ra được: \(\left\{{}\begin{matrix}c=-a-b\\d=2a+b\end{matrix}\right.\)
Thế vào pt cuối:
\(\dfrac{\left|3a-b\right|}{\sqrt{a^2+b^2+\left(a+b\right)^2}}=\dfrac{3}{\sqrt{2}}\)
\(\Rightarrow2\left(3a-b\right)^2=9\left(a^2+b^2\right)+9\left(a+b\right)^2\)
\(\Rightarrow15ab+8b^2=0\Rightarrow\left[{}\begin{matrix}b=0\\b=-\dfrac{15a}{8}\end{matrix}\right.\)
VL
1
AH
Akai Haruma
Giáo viên
18 tháng 1 2021
Lời giải:
Từ $0,75x-10y=7,5\Rightarrow y=\frac{3}{40}x-\frac{3}{4}$. Thay vào PT $(2)$ ta có:
$-0,5x+x(\frac{3}{40}x-\frac{3}{4})=5$
$\Leftrightarrow -\frac{5}{4}x+\frac{3}{40}x^2=5$
$\Leftrightarrow 3x^2-50x-200=0$
$\Leftrightarrow (x-20)(3x+10)=0$
$\Rightarrow x=20$ hoặc $x=-\frac{10}{3}$
Nếu $x=20$ thì $y=\frac{3}{40}x-\frac{3}{4}=\frac{3}{4}$
Nếu $x=-\frac{10}{3}$ thì $y=\frac{3}{40}x-\frac{3}{4}=-1$
Vậy..........
VV
1
VD
17 tháng 3 2022
Để hệ vô nghiệm thì
\(\dfrac{2m-1}{m+3}\ne\dfrac{5}{1}\\ \Leftrightarrow2m-1\ne5\left(m+3\right)\\ \Leftrightarrow m\ne-\dfrac{16}{3}\)
\(\dfrac{2m-1}{m+3}=\dfrac{3}{-4}\left(m\ne-3\right)\\ \Leftrightarrow-4\left(2m-1\right)=3\left(m+3\right)\\ \Leftrightarrow m=-\dfrac{5}{11}\left(tm\right)\)
24 tháng 2 2023
a: Khi m=-1 thì hệ sẽ là:
x-y=11 và 5x-3y=0
=>x=-33/2 và y=-55/2
b: Để hệ có nghiệm duy nhất thì 1/5<>-m/3
=>m/-3<>1/5
=>m<>-3/5
WA
2
25 tháng 6 2020
giải hpt: \(\hept{\begin{cases}x^2+2y-4x=0\\4x^2-4xy^2+y^4-2y+4=0\end{cases}}\)
Cộng hai vế lại với nhau ta có:
\(4x^2-4xy^2+y^4+x^2-4x+4=0\)
\(\Leftrightarrow\left(2x-y\right)^2+\left(x-2\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}2x-y^2=0\\x-2=0\end{cases}\Rightarrow\hept{\begin{cases}x=2\\y^2=4\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}x=2;y=2\left(tm\right)\\x=2;y=-2\end{cases}}\)
Thay x,y vào pt và tính
=> x=2 và y=2 thỏa mãn
=>(x;y)=(2;2) (t/m)
MN
25 tháng 6 2020
@Linh: Làm nhầm rồi
HPT\(\hept{\begin{cases}x^2+2y-4x=0\\4x^2-4xy^2+y^4-2y+4=0\end{cases}}\)
Cộng vế với vế của hai phương trình, ta được:
\(HPT\Leftrightarrow5x^2-4xy^2+y^2-4x+4=0\)
\(\Leftrightarrow\left(4x^2-4xy^2+y^2\right)+\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left(2x-y\right)^2+\left(x-2\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}2x-y=0\\x-2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2\\y=4\end{cases}}\)
Vậy \(\left(x;y\right)=\left(2;4\right)\)
19 tháng 9 2016
\(hpt\Leftrightarrow\begin{cases}y=\frac{60x^2}{36x^2+25}\\z=\frac{60y^2}{36y^2+25}\\x=\frac{60z^2}{36z^2+25}\end{cases}\)
Từ hệ suy ra x,y,z không âm. Nếu x=0 thì y=z=0 suy ra (0;0;0) là nghiệm của hệ phương trình.
Nếu x>0 thì y>0, z>0. Xét hàm số \(f\left(t\right)=\frac{60t^2}{36t^2+25},t>0\)
Ta có: \(f'\left(t\right)=\frac{3000t}{\left(36t^2+25\right)^2}>0\) với mọi t>0
Do đó \(f\left(t\right)\) đồng biến trên khoảng \(\left(0;+\infty\right)\)
Hệ pt đc viết lại \(\begin{cases}y=f\left(x\right)\\z=f\left(y\right)\\x=f\left(z\right)\end{cases}\)
Từ tính đồng biến của f(x) suy ra x=y=z. Thay vào hệ ta được
x(36x2-60x+25)=0. Chọn \(x=\frac{5}{6}\)
Vậy tập nghiệm của hệ pt là \(\left\{\left(0;0;0\right);\left(\frac{5}{6};\frac{5}{6};\frac{5}{6}\right)\right\}\)
LT
0
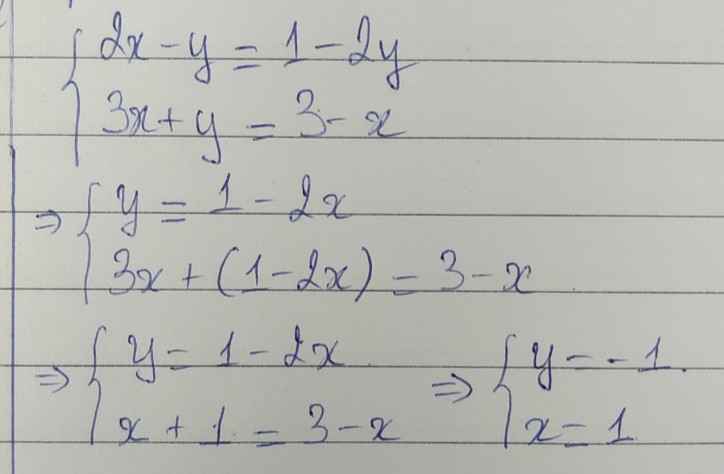
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{3}x+\dfrac{1}{3}-\dfrac{1}{4}y-\dfrac{1}{2}-\dfrac{2}{5}x+\dfrac{2}{5}y=0\\\dfrac{1}{4}x-\dfrac{3}{4}-\dfrac{1}{3}y+1-2y+x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{1}{15}x+\dfrac{3}{20}y=\dfrac{1}{6}\\\dfrac{5}{4}x-\dfrac{7}{3}y=-\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+3y=10\\15x-28y=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-60x+45y=150\\60x-112y=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{138}{67}\\x=\dfrac{1221}{335}\end{matrix}\right.\)