 Mọi người giúp em với, em cần gấp lắm rồi :((
Mọi người giúp em với, em cần gấp lắm rồi :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-3m+4\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-3m+4\right)\)
\(=4m^2-16m+4-4m^2+12m-16=-4m-12\)
Để phương trình có hai nghiệm phân biệt thì -4m-12>0
=>-4m>12
hay m<-3
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3m+4\end{matrix}\right.\)
Theo đề, ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow m^2-3m+4-2m+2=0\)
=>(m-2)(m-3)=0
hay \(m\in\varnothing\)

Tham khảo:
In a spell of dry weather, when the Birds could find very little to drink, a thirsty Crow found a pitcher with a little water in it.
But the pitcher was high and had a narrow neck, and no matter how he tried, the Crow could not reach the water. The poor thing felt as if he must die of thirst.
Then an idea came to him. Picking up some small pebbles, he dropped them into the pitcher one by one. With each pebble the water rose a little higher until at last it was near enough so he could drink.
“In a pinch a good use of our wits may help us out.”

Câu 1.
Khi mở khóa K:
\(I_m=I_1=0,4A\)
Khi đóng khóa K:
\(I_m=I_1+I_2=0,6\Rightarrow I_2=0,2A\)
\(U_1=0,4\cdot5=2V\)
\(\Rightarrow U_2=U_1=2V\)
\(\Rightarrow U=U_1=U_2=2V\)
\(R_2=\dfrac{U_2}{I_2}=\dfrac{2}{0,2}=10\Omega\)

a) \(P=\dfrac{\sqrt{x}+5}{\sqrt{x}-2}=\dfrac{\sqrt{9}+5}{\sqrt{9}-2}=\dfrac{3+5}{3-2}=8\)
b) \(Q=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-\dfrac{5\sqrt{x}-2}{4-x}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{x-3\sqrt{x}+2+5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
c) \(M=\dfrac{Q}{P}=\dfrac{\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+5}{\sqrt{x}-2}=\dfrac{\sqrt{x}}{\sqrt{x}-2}.\dfrac{\sqrt{x}-2}{\sqrt{x}+5}=\dfrac{\sqrt{x}}{\sqrt{x}+5}< \dfrac{1}{2}\)
\(\Leftrightarrow2\sqrt{x}< 3\sqrt{x}+15\Leftrightarrow\sqrt{x}>-15\left(đúng\forall x\ge0,x\ne4\right)\)
d) \(M=\dfrac{\sqrt{x}}{\sqrt{x}+5}=1-\dfrac{5}{\sqrt{x}+5}\in Z\)
\(\Rightarrow\sqrt{x}+5\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
Do \(x\ge0,x\ne4\)
\(\Rightarrow x\in\left\{0\right\}\)

Thay x = - 3 ; y = 4 vào hpt trên ta được
\(\left\{{}\begin{matrix}-3m-4=n\\-3n+4m=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n+3m=-4\\-3n+4m=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3n+9m=-12\\-3n+4m=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13m=-11\\n=-3m-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{11}{13}\\n=-\dfrac{19}{13}\end{matrix}\right.\)

\(1.\Rightarrow R1//R2\)
\(\Rightarrow U2=U1=\left(I-I2\right).R1=4,8V\Rightarrow R2=\dfrac{U2}{I2}=\dfrac{4,8}{0,4}=12\Omega\)
\(b,\Rightarrow U=U1=4,8V\)
\(c,R1//R2//R3\Rightarrow I3=I-1,2=0,3A\Rightarrow R3=\dfrac{4,8}{I3}=16\Omega\)
\(\Rightarrow Rtd=\dfrac{U}{I}=\dfrac{4,8}{1,5}=3,2\Omega\)
\(2.\left(R1ntR2\right)//R3\)
\(\Rightarrow Rtd=\dfrac{R3\left(R1+R2\right)}{R3+R1+R2}=5\Omega\)
\(b,\Rightarrow\left\{{}\begin{matrix}Im=\dfrac{U}{Rtd}=2A\\I3=\dfrac{U}{R3}=1A\\I1=I2=Im-I3=1A\\\end{matrix}\right.\)
\(c,\Rightarrow\left\{{}\begin{matrix}U3=U=10V\\U1=I1.R1=4V\\U2=10-4=6V\end{matrix}\right.\)

a: ΔOIK cân tại O
mà OD là đừog cao
nên D là trung điểm của IK
b: Xét ΔFDC vuông tại D và ΔFAE vuông tại A có
góc DFC=góc AFE
=>ΔFDC đồng dạng với ΔFAE
=>FD/FA=FC/FE
=>FD*FE=FC*FA
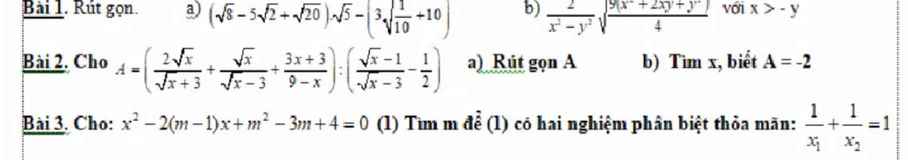







Bài 2:
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc 1 đường tròn(1)
Xét tứ giác OHAC có
\(\widehat{OHA}+\widehat{OCA}=180^0\)
Do đó: OHAC là tứ giác nội tiếp
=>O,H,A,C cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,B,H,O,C cùng năm trên 1 đường tròn
b: \(\widehat{BHA}=\widehat{BOA}\)
\(\widehat{CHA}=\widehat{AOC}\)
mà \(\widehat{AOB}=\widehat{AOC}\)
nên \(\widehat{BHA}=\widehat{CHA}\)
hay HA là tia phân giác của góc BHC
Làm hộ em bài 1 và 2 ảnh đầu tiên được không ạ?