Làm giúp em câu 54 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 5 2022
Para 1 - b
Para 2 - a
Para 3 - c
T - F - T - T - NG
1 B
2 A
3 D
4 D
5 A
25 tháng 10 2023
Câu 7:
a, \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\)
b, \(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
Theo PT: \(n_{Fe}=n_{H_2}=0,1\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,1.56}{10}.100\%=56\%\\\%m_{CuO}=44\%\end{matrix}\right.\)
c, \(n_{CuO}=\dfrac{10-0,1.56}{80}=0,055\left(mol\right)\)
Theo PT: \(n_{H_2SO_4}=n_{Fe}+n_{CuO}=0,155\left(mol\right)\)
\(\Rightarrow C\%_{H_2SO_4}=\dfrac{0,155.98}{100}.100\%=15,19\%\)
d, Theo PT: \(\left\{{}\begin{matrix}n_{FeSO_4}=n_{Fe}=0,1\left(mol\right)\\n_{CuSO_4}=n_{CuO}=0,055\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{FeSO_4}=0,1.152=15,2\left(g\right)\\m_{CuSO_4}=0,055.160=8,8\left(g\right)\end{matrix}\right.\)
25 tháng 10 2023
Câu 8:
a, \(CuCO_3+2HCl\rightarrow CuCl_2+CO_2+H_2O\)
b, \(n_{CO_2}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)
Theo PT: \(n_{CuCO_3}=n_{CO_2}=0,15\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CuCO_3}=\dfrac{0,15.124}{20}.100\%=93\%\\\%m_{CuCl_2}=7\%\end{matrix}\right.\)
c, \(n_{HCl}=2n_{CO_2}=0,3\left(mol\right)\)
\(\Rightarrow C_{M_{HCl}}=\dfrac{0,3}{0,2}=1,5\left(M\right)\)
MN
0
T
1
2 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
H
8 tháng 8 2021
Bài 2 : (1) liên kết ; (2) electron ; (3) liên kết ; (4) : electron ; (5) sắp xếp electron
Bài 4 :
$\dfrac{M_X}{4} = \dfrac{M_K}{3} \Rightarrow M_X = 52$
Vậy X là crom,KHHH : Cr
Bài 5 :
$M_X = 3,5M_O = 3,5.16 = 56$ đvC
Tên : Sắt
KHHH : Fe
H
8 tháng 8 2021
Bài 9 :
$M_Z = \dfrac{5,312.10^{-23}}{1,66.10^{-24}} = 32(đvC)$
Vậy Z là lưu huỳnh, KHHH : S
Bài 10 :
a) $PTK = 22M_{H_2} = 22.2 = 44(đvC)$
b) $M_{hợp\ chất} = X + 16.2 = 44 \Rightarrow X = 12$
Vậy X là cacbon, KHHH : C
Bài 11 :
a) $PTK = 32.5 = 160(đvC)$
b) $M_{hợp\ chất} = 2A + 16.3 = 160 \Rightarrow A = 56$
Vậy A là sắt
c) $\%Fe = \dfrac{56.2}{160}.100\% = 70\%$
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
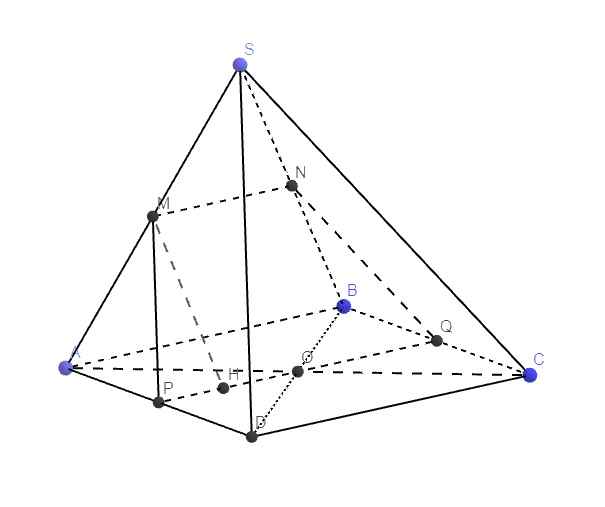
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
PN
0
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 6 2021
7a.
\(y'=3x^2-2\left(m-1\right)x-m-3\)
Hàm nghịch biến trên \(\left(-1;0\right)\) khi và chỉ khi \(y'\le0\) ; \(\forall x\in\left(-1;0\right)\)
\(\Leftrightarrow3x^2-2\left(m-1\right)x-m-3\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m-1\right)^2+3\left(m+3\right)>0\\x_1\le-1< 0\le x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+m+10>0\left(\text{luôn đúng}\right)\\f\left(-1\right)\le0\\f\left(0\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3+2\left(m-1\right)-m-3\le0\\-m-3\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2\le0\\-m-3\le0\end{matrix}\right.\) \(\Leftrightarrow-3\le m\le2\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 6 2021
7b.
\(y'=-x^2+2\left(m-1\right)x+m+3\)
Hàm đồng biến trên \(\left(0;3\right)\) khi và chỉ khi \(y'\le0\) ; \(\forall x\in\left(0;3\right)\)
\(\Leftrightarrow-x^2+2\left(m-1\right)x+m+3\ge0\) ; \(\forall x\in\left(0;3\right)\)
\(\Leftrightarrow m\left(2x+1\right)\ge x^2+2x-3\)
\(\Leftrightarrow m\ge\dfrac{x^2+2x-3}{2x+1}\)
\(\Leftrightarrow m\ge\max\limits_{\left[0;3\right]}\dfrac{x^2+2x-3}{2x+1}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+2x-3}{2x+1}\) trên \(\left(0;3\right)\)
\(f'\left(x\right)=\dfrac{2\left(x^2+x+4\right)}{\left(2x+1\right)^2}>0\) ; \(\forall x\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)< f\left(3\right)=\dfrac{12}{7}\)
\(\Rightarrow m\ge\dfrac{12}{7}\)
HT
1
vô cái cân = pthh là xong òi