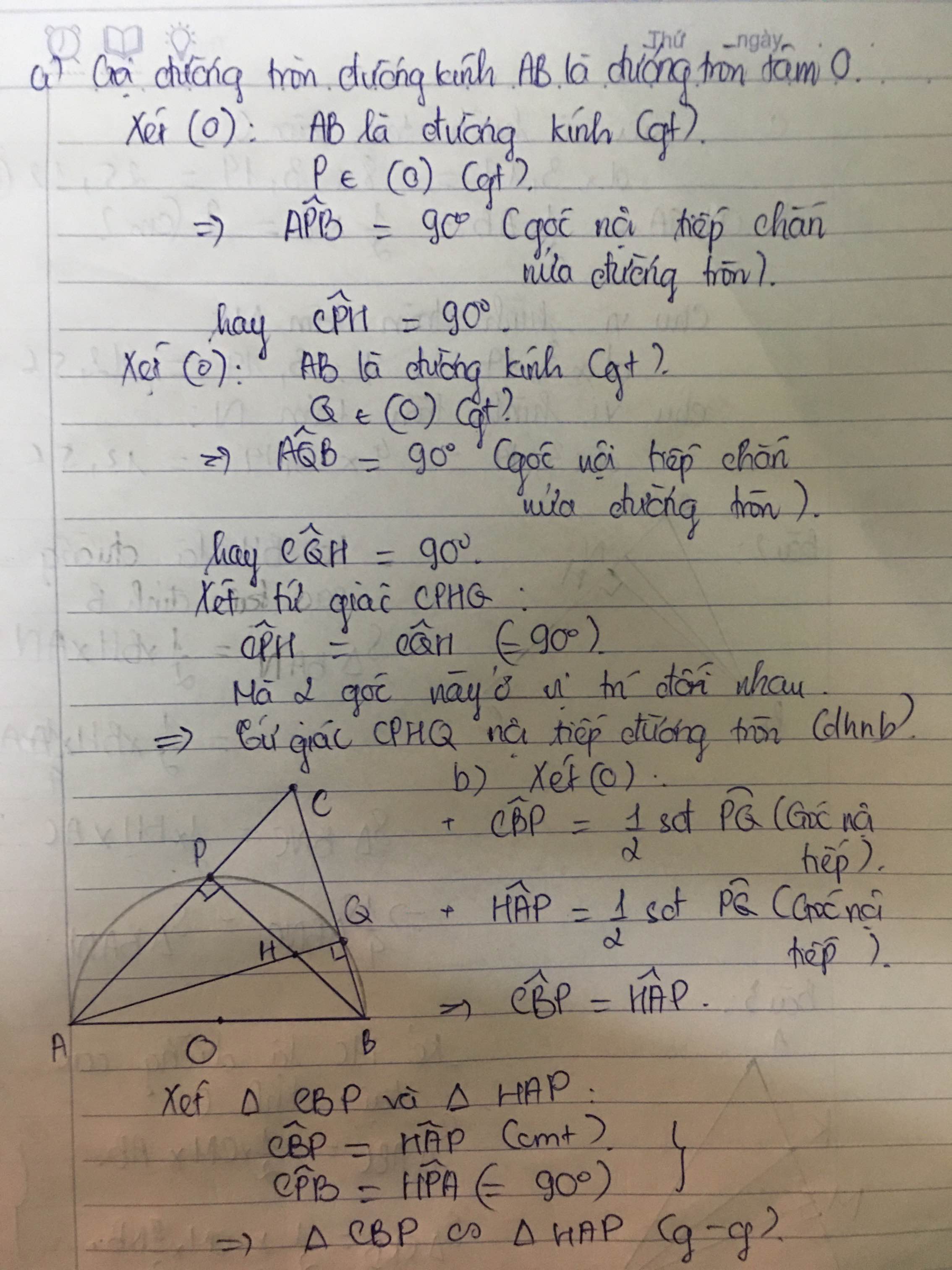Trên nửa đường tròn dường kính AB, lấy hai điểm P, Q sao cho P thuộc cung AQ. Gọi C là giao điểm của tia AP và tia BQ ; H là giao điểm của hai dây cung AQ và BP;
a, chứng minh tứ giác CPHQ nội tiếp đường tròn
b, chứng minh tam giác CBP đồng dạng với tam giác HAP
c, Biết AB=2R, tính theo RT giá trị của biểu thức : S=AP.AC+BQ.BC