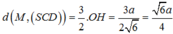Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA=2a và vuông góc với đáy . Tính góc giữa SA và (SBC) .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
10 tháng 1 2019
Đáp án D
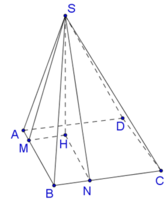
Gọi H là chân đường cao hạ từ S đến mặt phẳng (ABCD). Trong mặt phẳng (ABCD), kẻ HM,HN lần lượt vuông góc với AB,BC.

Vậy thể tích hình chóp S.ABCD là:
![]()

22 tháng 2 2021
gọi K thuộc SC sao cho DK \(\perp\) SC , BK \(\perp\)SC
=> ((SCD),(SBC)) = (DK,KB)
tính được SD = \(\frac{\sqrt{10}}{2}\)a, AC = \(\sqrt{3}\)a, SC= \(\frac{3\sqrt{2}}{2}\)a
\(DC^2=SD^2+SC^2-2SD.SC.cos\widehat{DSC}\)
=> \(\widehat{DSC}\)=....... (số xấu)
\(sin\widehat{DSC}\)= \(\frac{DK}{SD}\)=> DK = \(\frac{\sqrt{2}}{2}\)=BK
\(DB^2=DK^2+BK^2-2.DK.BK.cos\alpha\)=> \(\alpha=\frac{\pi}{2}\)

CM
29 tháng 10 2019
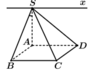
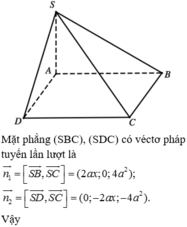
• Giao tuyến của (SBC) và (SAD) là
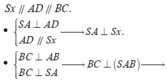
![]()
![]() (do tam giác SAB vuông cân).
(do tam giác SAB vuông cân).
Chọn B.