Tìm nghiệm nguyên ko âm của phương trình: x²=y²+y+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BM
0
CM
19 tháng 10 2018
Ta có 3x + 4y = −10 ⇔ 3x = −4y – 10 ⇔ x = − 4 y − 10 3 ⇔ x = − y − y + 10 3
Đặt y + 10 3 = t t ∈ ℤ ⇒ y = 3t – 10 ⇒ x = − (3t – 10) – t = −4t + 10
Hay nghiệm nguyên của phương trình 3x + 4y = −10 là x = − 4 t + 10 y = 3 t − 10 t ∈ ℤ
Vì x; y nguyên âm hay x < 0; y < 0 nên − 4 t + 10 < 0 3 t − 10 < 0 ⇔ t > 2 , 25 t < 10 3
mà t ∈ ℤ ⇒ t = 3
Suy ra x = −4.3 + 10 = −2; y = 3.3 – 10 = −1 nên nghiệm nguyên âm cần tìm là (a; y) = (−2; −1) ⇒ x.y = 2
Đáp án: A
NS
0
H
1
YN
19 tháng 4 2021
Vì 105 là số nguyên lẻ nên 2x+5y+1 và 2020lxl+y+x2+x là số lẻ
=> 5y chẵn => y chẵn
Có:x2+x=x(x+1) là số chẵn nên 2020lxl lẻ
=>x=0
Thay x=0 vào phương trình (2x+5y+1)(2020lxl+y+x2+x)=105 ta được:
\(\left(5y+1\right)\left(y+1\right)=105\Leftrightarrow5y^2+6y-104=0\)
Do \(y\in Z\)nên ta tìm ra y=4
Vậy phương trình có nghiệm là \(\left(x;y\right)=\left(0;4\right)\)
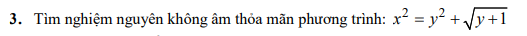
Bài này bạn sử dụng nguyên lý kẹp nhá.
Từ gt hãy kẹp x^2 giữa 2 bình phương, từ đó suy ra quan hệ của x và y. Bài này ngắn gọn hơn những bài khác là ở chỗ x, y không âm nên xét rất nhanh và ngắn gọn.