Cho a,b,c là độ dài 3 cạnh của tam giác.Chứng minh rằng:a^2+b^2+c^2 < 2 (ab+bc+ca)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AG
0
25 tháng 5 2018
Ta có (a-b)²≥0 nên a²+b²≥2ab, tương tự b²+c²≥2bc, c²+a²≥2ca, cộng vế với vế rồi chia 2 2 vế ta có a²+b²+c²≥ab+bc+ca
a, b, c là 3 cạnh tam giác nên a+b>c → c(a+b)>c², tương tự b(a+c)>b², a(b+c)>a², cộng vế với vế ta có 2(ab+bc+ca)>a²+b²+c²
25 tháng 5 2018
Áp dụng BĐT Cauchy cho 3 số không âm a^2 + b^2 + c^2 là ra nha bạn
K
1
LL
18 tháng 6 2015
Do a,b,c là độ dài cạnh tam giác nên:
a<b+c
b<c+a
c<a+b
ta co:
a^2b +b^2c+c^2a+ca^2+bc^2+ab^2
= a^2(b+c) + b^2(c+a) + c^2(a+b)
> a^2.a +b^2.b+c^2.c =a^3+b^3+c^3
<=> a^2b +b^2c+c^2a+ca^2+bc^2+ab^2 - a^3-b^3-c^3 > 0
LL
3 tháng 3 2019
Nếu Đặt p là nửa chu vi => p = (a + b + c)/2 => 2p = a + b + c
=> p - a = (a + b + c)/2 - a
=> p - a = (b + c + a - 2a)/2
=> p - a = (b + c - a)/2
=> 2(p - a) = b + c - a (1)
Tương tự ta chứng minh được:
2(p - b) = a + c - b (2)
2(p - c) = a + b - c (3)
Từ (1); (2) và (3) => 1/(a + b - c) + 1/(b +c - a) +1/(c +a - b)
= 1/[ 2(p - c) ] + 1/[ 2(p - a) ] + 1/[ 2(p - b) ]
=1/2.[ 1/(p - a) + 1/(p - b) + 1/(p - c) ]
Bây giờ ta đã đưa bài toán về chứng minh
1/2.[ 1/(p - a) + 1/(p - b) + 1/(p - c) ] ≥ 1/a + 1/b + 1/c
Ta có: (x - y)² ≥ 0
<=> x² - 2xy + y² ≥ 0
<=> x² - 2xy + y² + 4xy ≥ 4xy
<=> x² + 2xy + y² ≥ 4xy
<=> (x + y)² ≥ 4xy
=> với x + y ≠ 0 và xy ≠ 0
=> (x + y)²/(x+ y) ≥ 4xy/(x + y)
=> (x + y) ≥ 4xy/(x + y)
=> (x + y)/xy ≥ (4xy)/[xy(x + y)]
=> 1/x + 1/y ≥ 4/(x + y) (*)
Áp dụng (*) với x = p - a và y = p - b ta được:
1/(p - a) + 1/(p - b) ≥ 4/(p - a + p - b)
=> 1/(p - a) + 1/(p - b) ≥ 4/(2p - a - b)
=> 1/(p - a) + 1/(p - b) ≥ 4/(a + b + c - a - b)
=> 1/(p - a) + 1/(p - b) ≥ 4/c (4)
Chứng minh tương tự ta được:
1/(p - a) + 1/(p - c) ≥ 4/b (5)
1/(p - b) + 1/(p - c) ≥ 4/a (6)
Cộng vế với vế của (4);(5) và (6) ta được:
1/(p - a) + 1/(p - b) + 1/(p - a) + 1/(p - c) + 1/(p - b) + 1/(p - c) ≥ 4/c + 4/b + 4/a
=> 2.[ 1/(p - a) + 1/(p - b) + 1/(p - c) ] ≥ 4/c + 4/b + 4/a
=> 2.[ 1/(p - a) + 1/(p - b) + 1/(p - c) ] ≥ 4(1/a + 1/b + 1/c)
=> 1/(p - a) + 1/(p - b) + 1/(p - c) ≥ 2(1/a + 1/b + 1/c)
=> 1/2.[ 1/(p - a) + 1/(p - b) + 1/(p - c) ] ≥ 1/2.( 2(1/a + 1/b + 1/c) )
=> 1/2.[ 1/(p - a) + 1/(p - b) + 1/(p - c) ] ≥ 1/a + 1/b + 1/c
Dấu bằng xảy ra <=> a = b = c.
Sai thì thôi nha !!! k mk nha
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 7 2021
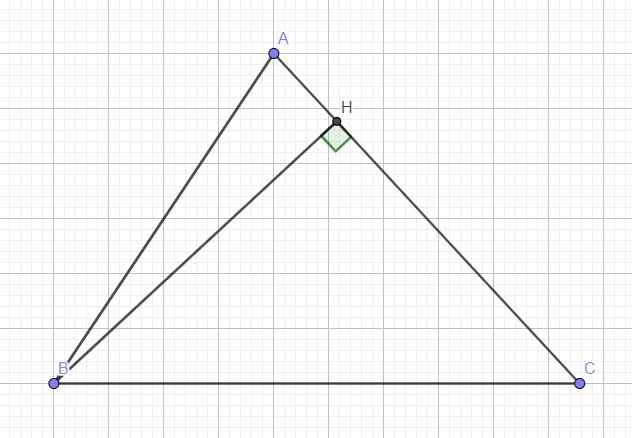
Kẻ đường cao BH (H thuộc AC)
Do góc A nhọn \(\Rightarrow\) H nằm giữa A và C
Ta có: \(S_{ABC}=\dfrac{1}{2}BH.AC\Leftrightarrow\dfrac{2}{5}bc=\dfrac{1}{2}BH.b\)
\(\Rightarrow BH=\dfrac{4c}{5}\)
Áp dụng Pitago cho tam giác vuông ABH:
\(AH^2=AB^2-BH^2=c^2-\left(\dfrac{4c}{5}\right)^2=\dfrac{9c^2}{25}\Rightarrow AH=\dfrac{3c}{5}\)
\(\Rightarrow CH=AC-AH=b-\dfrac{3c}{5}\)
Pitago tam giác vuông BCH:
\(BC=\sqrt{BH^2+CH^2}=\sqrt{\left(\dfrac{4c}{5}\right)^2+\left(b-\dfrac{3c}{5}\right)^2}=\sqrt{b^2-\dfrac{6}{5}bc+c^2}\)
a2+b2+c2<2(ab+bc+ac)
<=>a2+b2+c2-2ab-2ac-2bc<0
<=>a^2+b^2+c^2-2ab-2ac+2bc-4bc<0
<=>(a-b-c)2-4bc<0
Mà a,b,c là độ dài 3 cạnh của tam giác nên a-b-c<0=>(a-b-c)2<0(1)
bc>0=>4bc>0=>-4bc<0(2)
từ (1) và (2) =>(a-b-c)2-4bc<0
k cho mình nha
Theo BĐT tam giác:
(+) a+b > c
<=>(a+b).c > c2<=>ac+bc > c2 (1)
(+)a+c > b
<=>(a+c).b > b2<=>ab+bc > b2 (2)
(+)b+c > a
<=>(b+c).a > a2<=>ab+ac > a2 (3)
Cộng từng vế (1);(2);(3)
=>a2+b2+c2 < ac+bc+ab+bc+ab+ac=2ab+2bc+2ac=2(ab+bc+ca)
=>ĐPCM