Cho tam giác \(ABC\) có ba góc nhọn, các đường cao BD,CE cắt nhau tại H. Đường thẳng AH cắt BC tại F. CM: \(\frac{HF}{AF}+\frac{HD}{DC}+\frac{HE}{BE}=1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

3 tháng 5 2021
a,Xét tg DHB và tg DCA có: ^HDB=^CDA=90 độ, ^DBH=^DAC ( cùng phụ với hai góc bằng nhau BHD=^AHE)
Do đó: tg HDB đồng dạng tg DCA (g.g)
Suy ra: HD/DC=BD/DA-> bd*dc=dh*da
b, HD/HA=SBHC/SABC
HE/BE=SAHC/SABC
HF/CF=SHAB/SABC
HD/HA+HE/BE+HF/CF=SBHC/SABC+SAHC/SABC+SAHB/SABC=1

11 tháng 4 2019
Mấy câu trên bạn lm được rồi mimhf sẽ không giải nữa mà chỉ làm câu d thôi.
Ta có : các điểm D; E; F lần lượt nằm trên các cạnh AC; AB; BC
Mà 3 đoạn thẳng AF; BD; CE đồng quy tại H
Áp dụng định lý Ceeva vào tam giác ABC ta được:
EA/EB . FB/FC . DC/DA = 1
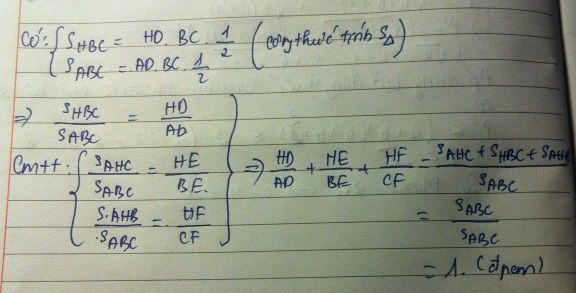
 đó nha bn
đó nha bn
Với \(AF;\) \(BD;\) \(CE\) lần lượt là ba đường cao ứng với các cạnh \(BC;\) \(AC;\) \(AB\) của \(\Delta ABC\), ta có:
\(\frac{S_{BHC}}{S_{ABC}}=\frac{\frac{1}{2}.HF.BC}{\frac{1}{2}.AF.BC}=\frac{HF}{AF}\) \(\left(1\right)\)
\(\frac{S_{AHC}}{S_{ABC}}=\frac{\frac{1}{2}.HD.AC}{\frac{1}{2}.CD.AC}=\frac{HD}{CD}\) \(\left(2\right)\)
\(\frac{S_{AHB}}{S_{ABC}}=\frac{\frac{1}{2}.HE.AB}{\frac{1}{2}.BE.AB}=\frac{HE}{BE}\) \(\left(3\right)\)
Cộng từng vế \(\left(1\right);\) \(\left(2\right)\) và \(\left(3\right)\), với chú ý rằng \(S_{BHC}+S_{AHC}+S_{AHB}=S_{ABC}\), ta được:
\(\frac{HF}{AF}+\frac{HD}{CD}+\frac{HE}{BE}=\frac{S_{BHC}+S_{AHC}+S_{AHB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Vậy, ....