hình vuông gọi là gì?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


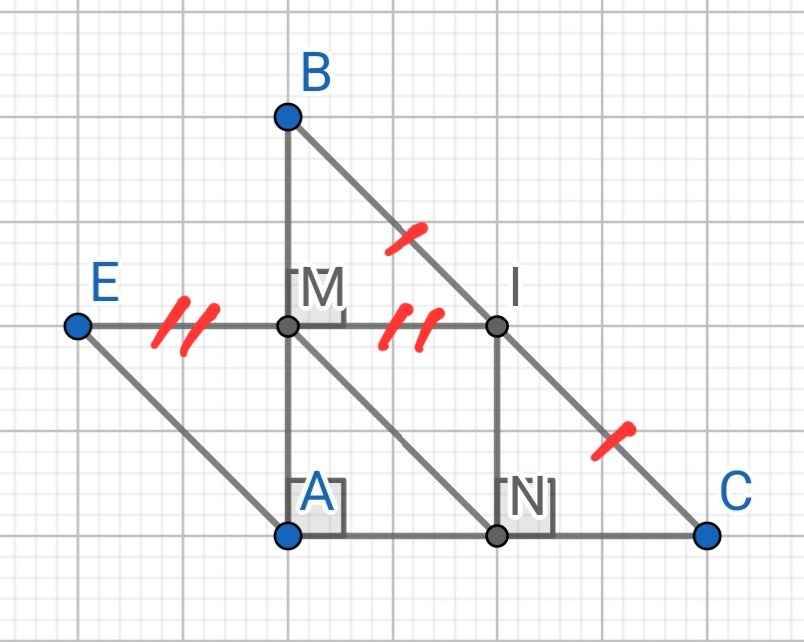
a) Do IM ⊥ AB (gt)
⇒ IM //AC
Mà I là trung điểm BC
⇒ M là trung điểm AB
⇒ IM là đường trung bình của ∆ABC
⇒ IM = AC/2
Do IN ⊥ AC (gt)
IN // AB
Mà I là trung điểm BC
⇒ N là trung điểm AC
⇒ AN = AC/2
⇒ IM = AC/2 = AN
Do IM // AC
⇒ IM // AN
Do M là trung điểm AB (cmt)
⇒ AM = IM = AB/2
Xét tứ giác AMIN có:
IM // AN (cmt)
IM = AN (cmt)
⇒ AMIN là hình bình hành
Mà ∠MAN = 90⁰ (∆ABC vuông tại A)
⇒ AMIN là hình chữ nhật
Lại có AM = IM (cmt)
⇒ AMIN là hình vuông
b) Do M là trung điểm AB (cmt)
N là trung điểm AC (cmt)
⇒ MN là đường trung bình của ∆ABC
⇒ MN // BC
c) Do E đối xứng với I qua M (gt)
⇒ ME = IM
⇒ ME = AN
Do IM // AN (cmt)
⇒ ME // AN
Xét tứ giác AEMN có:
ME // AN (cmt)
ME = AN (cmt)
⇒ AEMN là hình bình hành

a: Xét ΔABC có
M là trung điểm của BC
D là trung điểm của AB
Do đó: MD là đường trung bình
=>MD//AC và MD=AC/2
hay MK=AC và MK//AC
Xét tứ giác ADMC có MD//AC
nên ADMC là hình thang
mà \(\widehat{CAD}=90^0\)
nên ADMC là hình thang vuông
b: Xét tứ giác KMCA có
KM//AC
KM=AC
Do đó: KMCA là hình bình hành

a, N; P lần lượt là trung điểm của AC; BC (gt)
=> NP là đtb của tam giác ABC (Đn)
=> NP // AB (Đl)
=> góc PNA + CAB = 180 (đl)
có góc CAB = 90 do tam giác ABC vuông tại A (gt)
=> góc PNA = 90
chứng minh tương tự với góc PMA
=> NPMA Là hình chữ nhật
b, N đối xứng với E qua M (gt)
=> M là trung điểm của NE (đn)
M là trung điểm của AB (gt)
=> ANBE là hình bình hành (dấu hiệu)

a) AB=CD=2AD\Rightarrow AE=DF=AD
AE=DF=AD=FC; AE//DF \Rightarrow AEFD là hình thoi
AE//FC ; AE=FC \Rightarrow AECF là hình bình hành
b)c/m tương tự như câu a ta có BEFC là hình thoi
\Rightarrow góc M=góc N=90
mà EC//FA\Rightarrow góc E=N=M=F=90
\Rightarrow MENF là hình chữ nhật
c/nối MN
ENFM là hình vuông khi MN vuông góc EF
dễ dàng c/m dc MN//AB//CD \Rightarrow góc FEC=90\Rightarrow góc A=90
\Rightarrow ABCD là hình chữ nhật

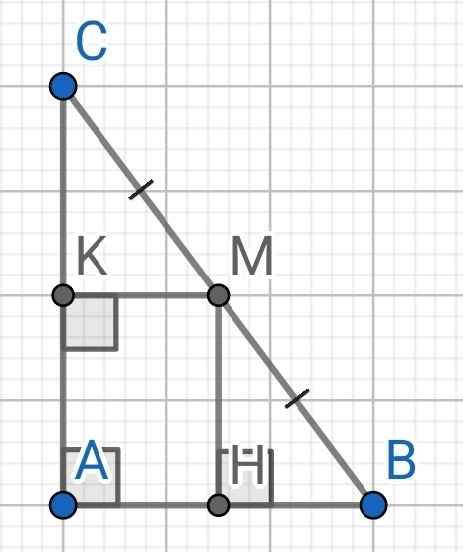 a) Do MH ⊥ AB (gt)
a) Do MH ⊥ AB (gt)
⇒ ∠AHM = 90⁰
Do MK ⊥ AC (gt)
⇒ ∠AKM = 90⁰
Tứ giác AHMK có:
∠AHM = ∠HAK = ∠AKM = 90⁰
⇒ AHMK là hình chữ nhật
b) AB = AC (gt)
⇒ ∆ABC vuông cân tại A
AM là đường trung tuyến
⇒ AM cũng là đường phân giác của ∆BAC
⇒ AM là đường phân giác của ∠HAK
Ta có:
AHMK là hình chữ nhật (cmt)
AM là đường phân giác của ∠HAK (cmt)
⇒ AHMK là hình vuông

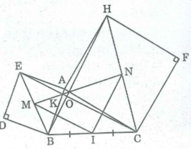
* Trong ∆ EBC , ta có: M là trung điểm EB (tính chất hình vuông)
I trung điểm BC (gt)
Nên MI là đường trung bình của ΔEBC
⇒ MI = 1/2 EC và MI // EC (tính chất đường trung bình của tam giác).
Trong ∆ BCH, ta có: I trung điểm BC (gt)
N trung điểm của CH (tính chất hình vuông)
Nên NI là đường trung bình của ∆ BCH
⇒ NI = 1/2 BH và NI // BH (tính chất đường trung bình của tam giác)
Mà BH = CE (chứng minh trên)
Suy ra: MI = NI nên ∆ INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay ∠ (MIN) = 90 0
Vậy ∆ MIN vuông cân tại I.



TL
Hình vuông gọi là square