Tìm các số nguyên tố a và b sao cho
abc<ab+ac+bc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tìm 3 số tự nhiên a, b, c sao cho cả 3 số abc, ab + bc + ca và a + b + c + 2 đều là các số nguyên tố


Giả sử a,b đều là số nguyên tố lớn hơn 3
=> a+b và a-b đều chẵn
Mà chỉ có 1 số nguyên tố chẵn là 2 => a+b=2 ; a-b=2
=>b=0. Mà 0 ko là số nguyên tố => b = 2
Ta có: a-2 ; a ;a+2 đều là số nguyên tố
=> a-2=3 ; a=5 ; a+2=7
=> a=5. Vậy a=5 b=7
để a-b là số nguyên tố thì a phải là số nguyên tố lớn hơn 3 (vì a=3 thì a-b=1 nếu b là số nguyên tố nhỏ nhất)
nếu a = 5 và b là số nguyên tố nhỏ nhất thì a+b=7 và a-b=3 là số nguyên tố (chọn)
nếu a là số nguyên tố lớn hơn 5 thì a+b hoặc a-b sẽ là hợp số
vậy a=5,b=2


Câu 1
a,b,c là số nguyên tố nên: a,b,c∈N∗và a,b,c≥2 Do đó,
ta có: c≥\(2^2\)+\(2^2\)>2 màc là số nguyên tố nên c phải là số lẻ:
Ta có: a\(a^b\)+\(b^a\)+3 là số lẻ nên tồn tại \(a^b\) hoặc b\(b^a\) chẵn mà a,b là số nguyên tố nên a=2 ∨ b=2 Xét 1 trường hợp, trường hợp còn lại tương tự: b=2 và a phải là số lẻ nên a=2k+1 k∈N∗
Ta có: \(2^a\)+\(a^2\)=c Nếu a=3 thì c=17 thỏa mãn. Nếu a>3 mà a là số nguyên tố nên a không chia hết cho 3 suy ra:\(a^2\)chia 3 dư 1. Ta có: \(2^a\)=\(2^{\left(k+1\right)}\)=\(4^k\).2−2+2=(\(4^k\)−1).2+2=BS(3)nên chia 3 dư 2 Từ đó, 2^a+a^2 ⋮3 nên c⋮3 suy ra c là hợp số, loại.
Vậy (a;b;c)=(2;3;17);(3;2;17)

Vì a, b, c có vai trũ như nhau nên giả sử a ≤ b ≤ c khi đó
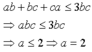
( Vì a là số nguyên tố )
Với a = 2 ta có
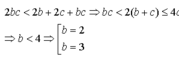
- Nếu b = 2 thì 4c < 2 + 4c thoả món với c là nguyên tố bất kỡ
- Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5
Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .

Bài 1:
Nếu p = 2 thì p + 2 = 2 + 2 = 4 không là số nguyên tố
2 + 4 = 6 không là số nguyên tố
Vậy p = 2 không thỏa mãn
Nếu p = 3 thì p + 2 = 3 + 2 = 5 là số nguyên tố
3 + 4 = 7 là số nguyên tố
Vậy p = 3 thỏa mãn
Nếu p > 3 thì p = 3k + 1 hoặc p = 3k + 2
Khi p = 3k + 1 thì p + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) không là số nguyên tố
Vậy p = 3k + 1 không thỏa mãn
Khi p = 3k + 2 thì p + 4 = 3k + 2 + 4 = 3k + 6 = 3(k + 2) không là số nguyên tố
Vậy p = 3k + 2 không thỏa mãn
Vậy p = 3 thỏa mãn duy nhất.
Bài 2:
Khi ta xét 3 số tự nhiên liên tiếp 4p; 4p + 1; 4p + 2 thì chắc chắn sẽ có một số chia hết cho 3
p là số nguyên tố; p > 3 nên p không chia hết cho 3 => 4p không chia hết cho 3
Ta thấy 2p + 1 là số nguyên tố; p > 3 => 2p + 1 > 3 nên 2p + 1 không chia hết cho 3 => 2(2p + 1) không chia hết cho 3 -> 4p + 2 không chia hết cho 3
Vì thế 4p + 1 phải chia hết cho 3
Mà p > 3 nên 4p + 1 > 3
=> 4p + 1 không là số nguyên tố. 4p + 1 là hợp số.


a, Do (a,b) = 6 => a = 6m; b = 6n với m,n ∈ N*; (m,n) = 1 và m ≤ n
Vì vậy ab = 6m.6n = 36mn, do ab = 216 => mn = 6. Do đó m = 1, n = 6 hoặc m = 2, n = 3
Với m = 1, n = 6 thì a = 6, b = 36
Với m = 2, n = 3 thì a = 12, b = 18
Vậy (a;b) là (6;36); (12;18)
b, Vì p là số nguyên tố nên ta xét các trường hợp của p
Trường hợp 1: p = 2, khi đó p+4 = 6; p+8 = 10 không là số nguyên tố (loại).
Trường hợp 2: p = 3, khi đó p+4 = 7; p+8 = 11 là hai số nguyên tố (thỏa mãn).
Trường hợp 3: p>3 nên p có dạng 3k+1; 3k+2 với k ∈ N*.
Nếu p = 3k+1 thì p+8 = 3k+1+8 = 3k+9 chia hết cho 3 và lớn hơn 3 nên p+8 không là số nguyên tố (loại).
Nếu p = 3k+2 thì p+4 = 3k+2+4 = 3k+6 chia hết cho 3 và lớn hơn 3 nên p+4 không là số nguyên tố (loại).
Kết luận. p = 3
Để câu trả lời của bạn nhanh chóng được duyệt và hiển thị, hãy gửi câu trả lời đầy đủ và không nên: