Lập bảng xét dấu f'(x) biết f(x) = |x2 - 2x - 3|
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2T
1
13 tháng 1 2023
Đặt f(x)=0
=>5x^2+4x-1=0
=>(x+1)(5x-1)=0
=>x=-1 hoặc x=1/5
=>f(x)<0 khi -1<x<1/5 và f(x)>0 khi x<-1 hoặc x>1/5
PT
1
CM
15 tháng 2 2018
f(x) = (3x2 – 10x + 3)(4x – 5)
+ Tam thức 3x2 – 10x + 3 có hai nghiệm x = 1/3 và x = 3, hệ số a = 3 > 0 nên mang dấu + nếu x < 1/3 hoặc x > 3 và mang dấu – nếu 1/3 < x < 3.
+ Nhị thức 4x – 5 có nghiệm x = 5/4.
Ta có bảng xét dấu:
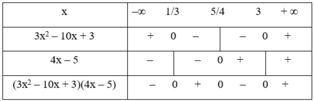
Kết luận:
f(x) > 0 khi x ∈ (1/3; 5/4) ∪ x ∈ (3; +∞)
f(x) = 0 khi x ∈ {1/3; 5/4; 3}
f(x) < 0 khi x ∈ (–∞; 1/3) ∪ (5/4; 3)
PT
1
CM
21 tháng 6 2017
f(x) = (3x2 – 4x)(2x2 – x – 1)
+ Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.
Do đó 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0
Do đó 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.
Ta có bảng xét dấu:
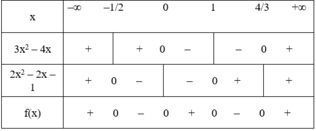
Kết luận:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
CM
7 tháng 11 2019
f(x) = (4x2 – 1)(–8x2 + x – 3)(2x + 9)
+ Tam thức 4x2 – 1 có hai nghiệm x = –1/2 và x = 1/2, hệ số a = 4 > 0
Do đó 4x2 – 1 mang dấu + nếu x < –1/2 hoặc x > 1/2 và mang dấu – nếu –1/2 < x < 1/2
+ Tam thức –8x2 + x – 3 có Δ = –95 < 0, hệ số a = –8 < 0 nên luôn mang dấu –.
+ Nhị thức 2x + 9 có nghiệm x = –9/2.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 khi x ∈ (–∞; –9/2) ∪ (–1/2; 1/2)
f(x) = 0 khi x ∈ {–9/2; –1/2; 1/2}
f(x) < 0 khi x ∈ (–9/2; –1/2) ∪ (1/2; +∞)
23 tháng 9 2023
Tham khảo:
Tam thức bậc hai \(f\left( x \right) = - {x^2} - 2x + 8\) có hai nghiệm phân biệt \({x_1} = - 4,{x_2} = 2\) và hệ số \(a = - 1 < 0\).
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
BB
2
23 tháng 2 2016
Có \(a=1>0;\Delta'=4>0;x_1=-5;x_2=-1\)
Lập bảng xét dấu :
| \(x\) | \(-\infty\) -5 -1 \(+\infty\) |
| \(f\left(x\right)\) | + 0 - 0 + |
23 tháng 2 2016
Từ bảng xét dấu trên ta có
\(T\left(f\left(x\right)=0\right)=\left\{-5;-1\right\};T\left(f\left(x\right)\ne0\right)=R\) / \(\left\{-5;-1\right\}\)
\(T\left(f\left(x\right)>0\right)=\left(-\infty;-5\right)\cup\left(-1;+\infty\right)\)
\(T\left(f\left(x\right)\ge0\right)=\left(-\infty;-5\right)\cup\left(-1;+\infty\right)\)
\(T\left(f\left(x\right)<0\right)=\left(-5;-1\right);T\left(f\left(x\right)\le0\right)=\left(-5;-1\right)\)
PT
1
23 tháng 2 2016
Có a=1>0; \(\Delta=-3<0\)
Bảng xét dấu :
| x | \(-\infty\) \(+\infty\) |
| \(f\left(x\right)\) | + |
Từ bảng xét dấu trên, ta được :
\(T\left(f\left(x\right)=0\right)=\varnothing;T\left(f\left(x\right)\ne0\right)=R;T\left(f\left(x\right)>0\right)=R;T\left(f\left(x\right)\ge0\right)=R\)
\(T\left(f\left(x\right)<0\right)=\varnothing;T\left(f\left(x\right)\le0\right)=\varnothing\)
VT
1
24 tháng 2 2016
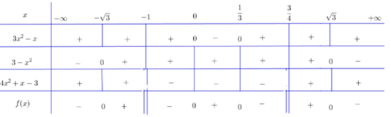
Ta có \(a=-5<0;\Delta'=16>0;x_1=-\frac{3}{5};x_2=1\)
Bảng xét dấu :
| \(x\) | \(-\infty\) \(-\frac{3}{5}\) 1 \(+\infty\) |
| \(f\left(x\right)\) | - 0 + - |
Từ bảng xét, ta được :
\(T\left(f\left(x\right)=0\right)=\left\{-\frac{3}{5};1\right\}\) ; \(T\left(f\left(x\right)\ne0\right)=R\)/ \(\left\{-\frac{3}{5};1\right\}\)
\(T\left(f\left(x\right)>0\right)=\left\{-\frac{3}{5};1\right\}\) ; \(T\left(f\left(x\right)\ge0\right)=\left[-\frac{3}{5};1\right]\)
Từ : \(T\left(f\left(x\right)<0\right)=\left(-\infty;-\frac{3}{5}\right)\cup\left(1;+\infty\right)\) ; \(T\left(f\left(x\right)\le0\right)=\left(-\infty;-\frac{3}{5}\right)\cup\left(1;+\infty\right)\)
24 tháng 2 2016
Đặt TT: = \(x^2+3x+2;MT:=-x^2+x+12\)
Lập bảng xét dấu TT và MT trên tập xác đinh D=R/\(\left\{-3;4\right\}\)
Từ đó suy ra dấu của f(x)
| x | -\(\infty\) -3 1 2 4 \(+\infty\) |
| TT | + + 0 - 0 + + |
| MT | - 0 + + + 0 - |
| f(x) | - // + 0 - 0 + // - |
Từ bảng xét dấu ta được
\(T\left(f\left(x\right)=0\right)=\left\{1;2\right\}\) ; \(T\left(f\left(x\right)\ne0\right)=R\) / \(\left\{-3;1;2;4\right\}\)
\(T\left(f\left(x\right)>0\right)=\left(3;1\right)\cup\left(2;4\right)\) ; \(T\left(f\left(x\right)\ge0\right)=\left(-3;1\right)\cup\left(2;4\right)\)
\(T\left(f\left(x\right)<0\right)=\left(-\infty;-3\right)\cup\left(1;2\right)\cup\left(4;+\infty\right)\)
\(T\left(f\left(x\right)\le0\right)=\left(-\infty;-3\right)\cup\left[1;2\right]\cup\left(4;+\infty\right)\)