Cho nửa đường tròn (O) đường kính AB. Điểm M nằm trên nửa đường tròn (M # A; B). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn (O) lần lượt tại C và D.
a) Chứng minh rằng tứ giác ACMO nội tiếp
b) Chứng minh rằng góc CAM bằng góc ODM
c) Gọi E là giao điểm của AM và BD; F là giao điểm của AC và BM. P là giao điểm của BA và DC. Chứng minh E; F; P thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
mà CM=CA
và DM=DB
nên CD=CA+DB

A B H M O D I K
a/
Ta có \(\widehat{AMB}=90^o\) (góc nt chắn nửa đường tròn)
Xét tg vuông AMB có
\(MH^2=AH.BH\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền = tích giữa các hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow BH=\dfrac{MH^2}{AH}=\dfrac{4^2}{2}=8cm\)
\(\Rightarrow AB=AH+BH=2+8=10cm\)
\(MA^2=AH.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow MA=\sqrt{AH.AB}=\sqrt{2.10}=2\sqrt{5}cm\)
\(MB^2=BH.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow MB=\sqrt{BH.AB}=\sqrt{8.10}=4\sqrt{5}cm\)
b/ Không rõ bạn hỏi biểu thức nào?
c/
Ta có \(OD\perp AM\) (2 tiếp tuyến cùng xuất phát từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm đường tròn vuông góc với dây cung nối 2 tiếp điểm)
Xét tg vuông AIO
Gọi K là trung điểm của AO => AK=OK
\(\Rightarrow IK=AK=OK=\dfrac{1}{2}AO\) không đổi (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Ta có
A; O cố định => K cố định; IK không đổi => khi M di chuyển trên nửa (O) => I chạy trên nửa đường tròn tâm K

a: Xét hình thang AHKB có
O là trung điểm của AB
OM//AHKB
Do đó: M là trung điểm của HK
b: Kẻ MN vuông góc với AB
Xét tứ giác AHMN có \(\widehat{AHM}+\widehat{ANM}=180^0\)
=>AHMN là tứ giác nội tiếp
=>\(\widehat{MAN}=\widehat{MHN}\)
Xét tứ giác MNBK có \(\widehat{MNB}+\widehat{MKB}=180^0\)
=>MNBK nội tiếp
=>\(\widehat{MBN}=\widehat{MKN}\)
Xét (O) có
ΔMAB nội tiếp
AB là đường kính
Do đó: ΔMAB vuông tại M
=>\(\widehat{MAB}+\widehat{MBA}=90^0\)
=>\(\widehat{NHK}+\widehat{NKH}=90^0\)
=>ΔNKH vuông tại N
ΔNKH vuông tại N có NM là trung tuyến
nên MH=MN
Xét (M) có
MN là bán kính
AB vuông góc MN tại N
Do đó: AB là tiếp tuyến của (M)
=>ĐPCM

1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK


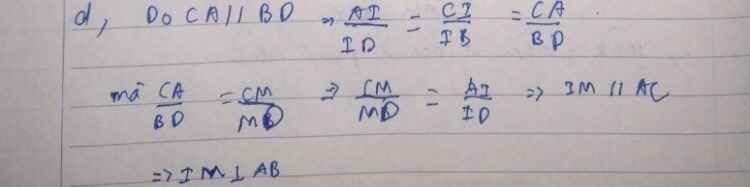
a: Xét tứ giác ACMO có
\(\widehat{CAO}+\widehat{CMO}=180^0\)
Do đó: ACMO là tứ giác nội tiếp
b:
Xét tứ giác DMOB có
\(\widehat{DMO}+\widehat{DBO}=180^0\)
Do đó: DMOB là tứ giác nội tiếp
Suy ra: \(\widehat{ODM}=\widehat{OBM}\)
mà \(\widehat{OBM}=\widehat{CAM}\left(=\dfrac{1}{2}sđ\stackrel\frown{AM}\right)\)
nên \(\widehat{CAM}=\widehat{ODM}\)