Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

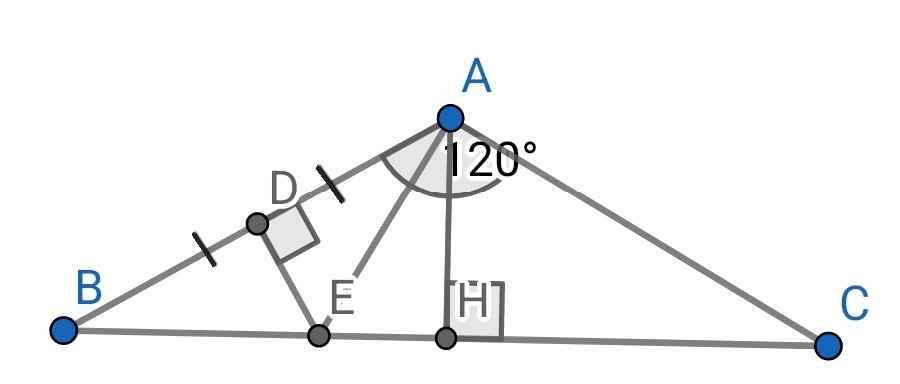 Do ∆ABC cân tại A (gt)
Do ∆ABC cân tại A (gt)
⇒ ∠B = ∠C = (180⁰ - ∠BAC) : 2
= (180⁰ - 120⁰) : 2
= 30⁰
∆AHB vuông tại H (do AH ⊥ BC)
⇒ ∠B + ∠BAH = 90⁰
⇒ ∠BAH = 90⁰ - ∠B
= 90⁰ - 30⁰
= 60⁰
Xét hai tam giác vuông: ∆AED và ∆BED có:
ED là cạnh chung
AD = BD (do D là trung điểm của AB)
⇒ ∆AED = ∆BED (hai cạnh góc vuông)
⇒ ∠EAD = ∠EBD = 30⁰ (hai góc tương ứng)
⇒ ∠EAH = ∠BAH - ∠EAD
= 60⁰ - 30⁰
= 30⁰
⇒ ∠EAH = ∠EAD
Xét hai tam giác vuông: ∆AEH và ∆AED có:
AE là cạnh chung
∠EAH = ∠EAD = 30⁰
⇒ ∆AEH = ∆AED (cạnh huyền - góc nhọn)
Mà ∆AED = ∆BED (cmt)
⇒ ∆BED = ∆AEH

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
mà B,H,C thẳng hàng(gt)
nên H là trung điểm của BC(Đpcm)
b) Xét ΔAMB và ΔCME có
\(\widehat{AMB}=\widehat{CME}\)(hai góc đối đỉnh)
MA=MC(M là trung điểm của AC)
\(\widehat{BAM}=\widehat{ECM}\)(hai góc so le trong, AB//CE)
Do đó: ΔAMB=ΔCME(g-c-g)
Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC(M là trung điểm của AC)
AH là đường trung tuyến ứng với cạnh BC(H là trung điểm của BC)
BM cắt AH tại I(gt)
Do đó: I là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
Ta có H là trung điêm BC => BH = CH = \(\dfrac{BC}{2}=\dfrac{12}{2}=6cm\)
Xét tam giác ABC cân tại H, H là trung điểm BC => H là đg cao => AH vuông góc với BC
Xét tam giác AHB có: AB2 = AH2 + HB2 (Py-ta-go)
Thay số: 202 = AH2 + 62
=> AH2 = 364 => AH = \(2\sqrt{91}\)
Xét tam giác ABH à tam giác ACH có
AH chung
AB = AC ( tam giác ABC cân tại A)
HB = HC =6cm (H là t/đ của BC)
➜tam giác ABH = tam giác ACH (c.c.c)
➜góc \(H_1\) = góc \(H_2\)
mà góc h1 + góc h2 = 180 độ (kề bù)
➜góc h1 = góc h2 = 90 độ
➜AH vuông góc với BC
Xét tam giác abh vuông tại h (cmt)
➜\(AB^2=AH^2+BH^2\)
➜\(AH^2=AB^2-BC^2\)
\(AH^2\)= \(20^2-6^2\)
\(AH^2\)= 364
AH > 0 ➜AH = \(\sqrt{364}\)