cho tam giác ABC cân tại A. Tia phân giác góc A cắt đường trung tuyến BD tại K. Gọi I là trung điểm của ab. Chứng minh rằng 3 điểm IKC thẳng hàng????
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 10 2017
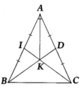
Vì tam giác ABC cân tại A nên tia phân giác AK đồng thời là đưòng trung tuyến.
Mà BD là trung tuyến của tam giác ABC nên K là trọng tâm của tam giác ABC.
Do đó I, K, C thẳng hàng
19 tháng 6 2020
tự kẻ hình nha
đặt AM là tia phân giác của BAC
xét tam giác ABM và tam giác ACM có
BAM=CAM(gt)
AB=AC(gt)
ABC=ACB(gt)
=> tam giác ABM= tam giác ACM(gcg)
=> BM=CM(hai cạnh tương ứng)
=> M là trung điểm của BC=> AM là trung tuyến
vì I là trung điểm AB=> CI là trung tuyến
vì BD giao AM tại K mà BD, AM là trung tuyến=> K là trọng tâm
mà CI là trung tuyến => K thuộc CI=> I,K,C thẳng hàng
4 tháng 4 2017
Gọi AE là phân giác của góc A( E thuộc BC)
Xét tam giác BAE và tam giác CAE có
AB=AC ( vì tam giác ABC cân tại A)
BAE=EAC( vì AD là tia phân giác của góc A)
Cạnh AE chung
=> Tam giác BAE= tam giác CAE
=>BE=EC
=> E là trung điểm của BC
=> AE là trung tuyến của BC
Ta có K là giao của 2 trung tuyến AD và BD
=> K là trọng tâm của tam giác ABC
Có I là trung điểm của AB
=>CI là trung tuyến của tam giác ABC
=>C,I,K thẳng hàng
