Hàm số y=x3-3x2+1 đồng biến trên những khoảng nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A
Tập xác định: D = ℝ
Đạo hàm: y ' = 3 x 2 - 6 x - 9
![]()
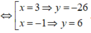
Bảng biến thiên
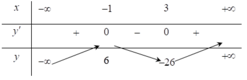
Hàm số đồng biến trên các khoảng - ∞ ; - 1 v à 3 ; + ∞
Do đó hàm số đồng biến trên khoảng 4 ; 5

Đáp án A.
y’ = -3x2 + 6x
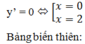

Vậy hàm số đồng biến trên khoảng (0; 2)

Chọn D.
TXĐ: D = R
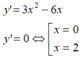
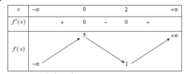
Từ bảng biến thiên suy ra hàm số đồng biến trên các khoảng (- ∞ ;0) và (2;+ ∞ )

Đáp án B.
Hàm số đồng biến khi y ' > 0 ⇔ 3 x 2 + 6 x > 0 ⇔ x > 0 x < − 2 .
ta có
\(y'=3x^2-6x=3x\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
y' >0 khi \(x\in\left(-\infty,0\right)\cup\left(2,+\infty\right)\)
Vậy hàm đồng biến trên hai khoảng là \(\left(-\infty,0\right)\cup\left(2,+\infty\right)\)