Tìm các cặp số tự nhiên x,y thỏa mãn 1+x+3x2+x3=y3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PD
1
AH
Akai Haruma
Giáo viên
9 tháng 7 2023
Lời giải:
PT $\Leftrightarrow x^3+x+1-y(x^2-3)=0$
$\Leftrightarrow y=\frac{x^3+x+1}{x^2-3}$ (hiển nhiên $x^2-3\neq 0$ với mọi $x$ nguyên)
Để $y$ nguyên thì $\frac{x^3+x+1}{x^2-3}$ nguyên
$\Leftrightarrow x^3+x+1\vdots x^2-3$
$\Rightarrow x(x^2-3)+4x+1\vdots x^2-3$
$\Rightarrow 4x+1\vdots x^2-3$
Hiển nhiên $4x+1\neq 0$ nên $|4x+1|\geq x^2-3$
Nếu $x\geq \frac{-1}{4}$ thì $4x+1\geq x^2-3$
$\Leftrightarrow x^2-4x-4\leq 0$
$\Leftrightarrow (x-2)^2\leq 8<9$
$\Rightarrow -3< x-2< 3$
$\Rightarrow -1< x< 5$
$\Rightarrow x\in \left\{0; 1; 2; 3; 4\right\}$.
Nếu $x< \frac{-1}{4}$ thì $-4x-1\geq x^2-3$
$\Leftrightarrow x^2+4x-2\leq 0$
$\Leftrightarrow (x+2)^2-6\leq 0$
$\Leftrightarrow (x+2)^2\leq 6< 9$
$\Rightarrow -3< x+2< 3$
$\Rightarrow -5< x< 1$
$\Rightarrow x\in\left\{-4; -3; -2; -1\right\}$
Đến đây bạn thay vào tìm $y$ thôi
NT
0
LT
0
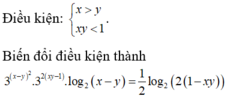
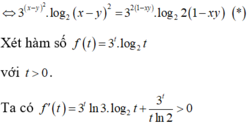
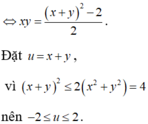
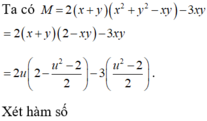
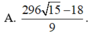
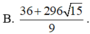
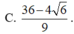
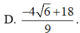
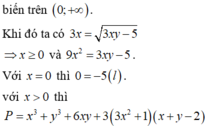
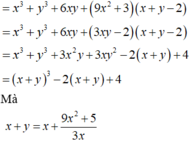
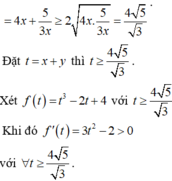
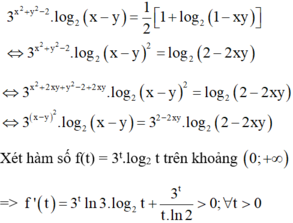
theo bài ra ta có
n = 8a +7=31b +28
=> (n-7)/8 = a
b= (n-28)/31
a - 4b = (-n +679)/248 = (-n +183)/248 + 2
vì a ,4b nguyên nên a-4b nguyên => (-n +183)/248 nguyên
=> -n + 183 = 248d => n = 183 - 248d (vì n >0 => d<=0 và d nguyên )
=> n = 183 - 248d (với d là số nguyên <=0)
vì n có 3 chữ số lớn nhất => n<=999 => d>= -3 => d = -3
=> n = 927