Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm; đường phân giác BI.Kẻ IH
vuông góc BC(H thuộc BC),gọi K là giao điểm của AB và IH
a) Tính BC
b)C/m : BK=BC,từ đó suy ra BI là đường trụng trực của KC
c)C/m:IB+IC+IK<20
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
H9
HT.Phong (9A5)
CTVHS
29 tháng 10 2023
Xét tam giác ABC vuông tại A áp dụn Py-ta-go ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có: \(sinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=90^o-53^o\approx37^o\)
PT
1
CM
14 tháng 1 2018
b. Vì AB < AC < BC ⇒ ∠C < ∠B < ∠A (quan hệ giữa góc và cạnh đối diện trong tam giác)
16 tháng 2 2022
Ta có:
\(AB^2+AC^2=8^2+6^2=64+36=100\left(cm\right)\)
\(BC^2=10^2=100\left(cm\right)\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A (định lý Pi-ta-go đảo)
16 tháng 2 2022
Áp dụng định lý Pytago đảo ta có:
AB2+AC2=82+62=100
mà 102=100
⇒82+62=102hay AB2+AC2=BC2
vậy ABC là tam giác vuông tại A
10 tháng 3 2022
a: BC=10cm
b: Xét ΔABK vuông tại A và ΔHBK vuông tại H có
BK chung
\(\widehat{ABK}=\widehat{HBK}\)
Do đó: ΔABK=ΔHBK
8 tháng 2 2021
1) Ta có: \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
Do đó: \(BC^2=AB^2+AC^2\)(=100)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
2) Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
3) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
SZ
1
A
2
KV
14 tháng 9 2023
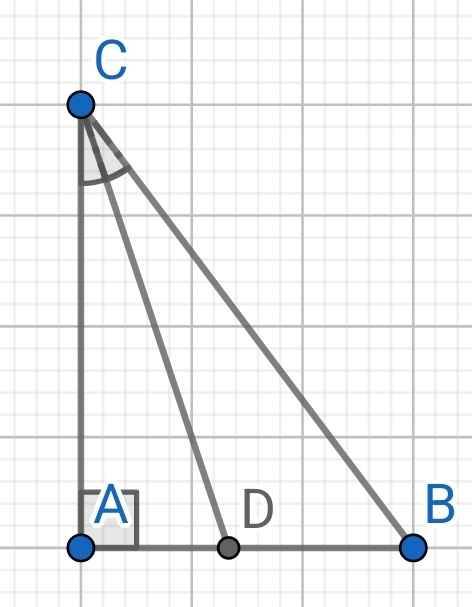Do ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do CD là phân giác (gt)
⇒ AD/AC = BD/BC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AD/AC = BD/BC = (AD + BD)/(AC + BC) = AB/(AC + BC) = 6/18 = 1/3
AD/AC = 1/3 ⇒ AD = AC.1/3 = 8/3 (cm)
∆ACD vuông tại A
⇒ CD² = AC² + AD² (Pytago)
= 8² + (8/3)²
= 640/9
⇒ CD = 8√10/3 (cm)
4 tháng 3 2021
Xét \(\Delta ABC\)vuông tại A theo định lí Pitago ta có : \(AB^2+AC^2=BC^2\Rightarrow6^2+8^2=BC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét \(\Delta DEF\)vuông tại D theo định lí Pitago ta có :\(DE^2+DF^2=EF^2\)
=> \(DF^2=EF^2-DE^2=15^2-9^2=144\)
=> \(DF=\sqrt{144}=12\left(cm\right)\)
Để hai tam giác trên đồng dạng với nhau , trước hết tính tỉ lệ tương ứng với 3 cạnh
Xét tam giác ABC và tam giác DEF ta có :
\(\frac{AB}{DE}=\frac{6}{9}=\frac{2}{3}\)
\(\frac{BC}{EF}=\frac{10}{15}=\frac{2}{3}\)
\(\frac{AC}{DF}=\frac{8}{12}=\frac{2}{3}\)
=> \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\left(=\frac{2}{3}\right)\)
=> Tam giác ABC đồng dạng tam giác DEF
Nếu bạn muốn làm tam giác DEF đồng dạng với tam giác ABC cũng được
KV
14 tháng 9 2023
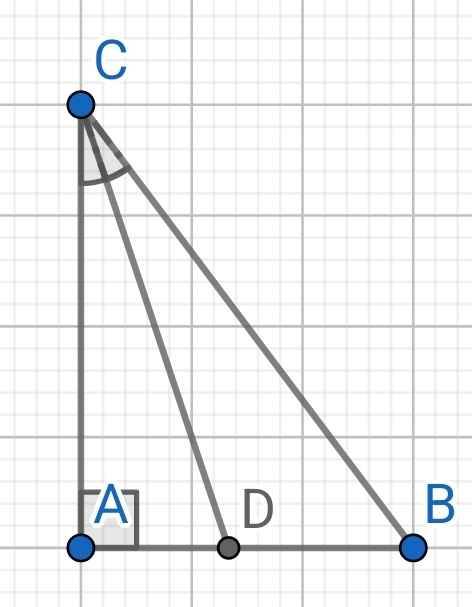∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do CD là phân giác của ∆ABC (gt)
⇒ AD/AC = BD/BC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AD/AC = BD/BC = (AD + BD)/(AC + BC) = AB/(AC + BC) = 6/18 = 1/3
AD/AC = 1/3 ⇒ AD = AC . 1/3 = 8/3 (cm)
∆ACD vuông tại A
⇒ CD² = AD² + AC² (Pytago)
= (8/3)² + 8²
= 640/9
⇒ CD = 8√10/3 (cm)
a) Mk bít làm mỗi phần a thui à
.Vì tam giác ABC vuông tại A
=> AB2 + AC2 =BC2
+) AB =6 cm
+) AC = 8 cm
=> 62 + 82 = BC2
=> 36 + 64 = BC2
=> 100 = BC2
=> BC= \(\sqrt{100}\) = 10 (cm)
Vậy BC = 10 cm