iết ab = 20 và a + b = – 9. Giá trị của biểu thức B = 2a³ + 2b³ là
– 189
2538
– 378
– 1269
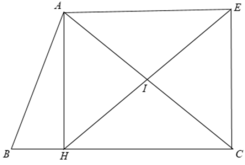
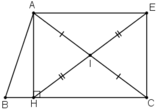
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm AC, E đối xứng với H qua I. Tứ giác AHCE là
Hình chữ nhật
Hình thoi
Hình bình hành
Hình vuông
Xóa lựa chọn
4cm
6cm
3cm
5cm
Trong các hình sau hình nào có tâm đối xứng
Hình bình hành
Tam giác đều
Hình thang cân
Hình thang vuông
Cho tam giác CDE. Trên cạnh DE lấy điểm K sao cho DK = 2KE. Ta có
..
,
,,
.
Giá trị lớn nhất của biểu thức C = 5x – x² là
– 25
– 6,25
25
6,25
Kết quả của phép tính (8x³ – 1) : (2x – 1) là
4x² + 2x + 1
– 4x²– 2x – 1
4x² – 2x – 1
4x² – 2x + 1
12cm²
18cm²
24cm²
6cm²
Chọn phát biểu SAI
Cả ba câu đều sai
Số 1 là phân thức đại số
Mỗi đa thức là một phân thức đại số
Số 0 là phân thức đại số
Để x(x²– 25) = 0 thì x bằng
5; -5
0; 25
0; 5; -5
0; 25; -25
Kết quả của phép tính 2,5.87,5 + 25.1,25 là:
20
250
200
25
Hình chữ nhật có đường chéo tạo với một cạnh một góc 30º. Đường chéo của hình chữ nhật đó dài 4cm. Diện tích của hình chữ nhật đó là
..
.
,,
,
.
,,
..
,
Cho tam giác ABC có chu vi là 8cm. Gọi tam giác A’B’C’ đối xứng với tam giác ABC qua đường thẳng d. Chu vi tam giác A’B’C’ là:
Một giá trị khác
16cm
8cm
6cm
2
4
8
16
Không có giá trị nào của n
1; 2; 3
1; 2
0; 1; 2; 3
..
,,
,
.
Phân tích đa thức 4x² – 25y² thành nhân tử ta được
(4x – 5y) ²
(4x – 25y)(4x + 25y)
(2x² – 5y²)(2x + 5y)
(2x – 5y)(2x + 5y)
Kết quả của phép chia 8x²y⁴ : 2x²y³ là:
4y
4xy
4xy²
2y
Giá trị của a để đa thức 2x² – 3x + a chia hết cho đa thức x – 2 là
4
2
–2
3
Số đo mỗi góc của lục giác đều là
60º
120º
108º
100º





Câu 1: B
Câu 2: A
Câu 3: C
Câu 4: D
Câu 5: A
Câu 6: B