Cho tam giác ABC có A(1,2), B(3,5), C(-2,4). Độ dài đường cao AH của tam giác là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
*) AH là đường cao của tam giác ABC.
*) Lập phương trình cạnh BC
B(1;-1), C(5;2) 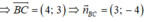
(BC): 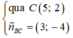
⇒ 3.(x - 5) - 4.(y - 2) = 0 ⇔ 3x - 15 - 4y + 8 = 0 ⇔ 3x - 4y - 7 = 0
Ta có:
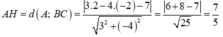

a: Xet ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng vói ΔBHA
b: ΔABC vuông tại A có AH vuông góc BC
nên AB*AC=AH*BC
c: \(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
AH=6*8/10=4,8cm
CH=8^2/10=6,4cm

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>góc BAH=góc CAH
=>AH là phân giác của góc BAC
c: BH=CH=3cm
AH=căn 5^2-3^2=4cm

\(\overrightarrow{BC}=\left(-4;-4\right)=-4\left(1;1\right)\)
Phương trình BC: \(1\left(x-4\right)-1\left(y-1\right)=0\Leftrightarrow x-y-3=0\)
Phương trình AH qua A và vuông góc BC:
\(1\left(x-1\right)+1\left(y-2\right)=0\Leftrightarrow x+y-3=0\)
H là giao điểm AH và BC nên tọa độ thỏa mãn: \(\left\{{}\begin{matrix}x-y-3=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow H\left(3;0\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(2;-2\right)\Rightarrow AH=2\sqrt{2}\)

mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
\(\overrightarrow{BC}=\left(-5;-1\right)\)
\(\overrightarrow{AH}=\left(x_H-1;y_H-2\right)\)
\(\overrightarrow{BH}=\left(x_H-3;y_H-5\right)\)
Theo đề, ta có: \(\left\{{}\begin{matrix}-5x_H+5-y_H+2=0\\-x_H+3=-5y_H+25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-5x_H-y_H=-3\\-5x_H+25y_H=110\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-26y_H=-113\\-x_H+5y_H=22\end{matrix}\right.\)
Đến đây bạn chỉ cần tìm tọa độ điểm H, xong rồi bạn áp dụng công thức \(AH=\sqrt{\left(x_H-x_A\right)^2+\left(y_H-y_A\right)^2}\) la ra