Công thức tính tốc độ trung bình trên một quãng đường và trên 2 quãng đường?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
15 tháng 8 2018
Vận tốc trung bình của người này trên cả hai quãng đường s 1 và s 2 là: V T B = S 1 + S 2 t 1 + t 2
⇒ Đáp án B
B.
D.Công thức A và B đúng.
20 tháng 10 2021
Đổi: 120m = 0,12km, 60s = 1h
Vận tốc tb của người đó trên quãng đường đầu:
\(v_1=\dfrac{S_1}{t_1}=\dfrac{0,12}{1}=0,12\left(km/h\right)\)
Vận tốc trên cả 2 quãng đường:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{0,12+4,5}{1+0,5}=3,08\left(km/h\right)\)
31 tháng 1 2022
- Tóm tắt:
s1=3km.
v1=6km/h.
s2=1,5km.
t2=0,5h.
______________
A. t1=?h.
B. v2=?km/h.
C. vtb=?km/h.
- Bài làm:
Thời gian đi trên quãng đường thứ nhất:
\(v_1=\dfrac{s_1}{t_1}\)=>\(t_1=\dfrac{s_1}{v_1}=\dfrac{3}{6}=0,5\) (h).
Tốc độ người đó đi trên quãng đường thứ hai:
\(v_2=\dfrac{s_2}{t_2}=\dfrac{1,5}{0,5}=3\) (km/h).
Tốc độ trung bình người đó trên cả hai quãng đường:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{3+1,5}{0,5+0,5}=4,5\) (km/h).
27 tháng 12 2021
Thời gian đi quãng đường đầu và quãng đường sau là:
\(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{24}\left(h\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2v_2}=\dfrac{S}{40}\left(h\right)\end{matrix}\right.\)
Vận tốc trung bình là: \(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{24}+\dfrac{S}{40}}=\dfrac{S}{S\left(\dfrac{1}{24}+\dfrac{1}{40}\right)}=15\left(\dfrac{km}{h}\right)\)
VT
31 tháng 12 2018
Chọn C
Công thức tính vận tốc trung bình của người này trên hai quãng đường s1 và s2 là:
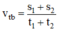
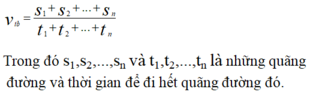
\(v_{tb}=\dfrac{s'+s}{t'+t}\\ v_{tb}=\dfrac{s}{t}\)
vtb=s′+st′+tvtb=st