Để hệ phương trình
\(4x-3y=7\)
\(2x^2+5y^2=m\)
có nghiệm thì điều kiện của m là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
0
16 tháng 2 2017
Câu 1 : \(a,\hept{\begin{cases}4x+7y=16\left(1\right)\\4x-3y=-24\left(2\right)\end{cases}}\)
Lấy ( 1 ) trừ ( 2 ) ta được :
10y = 40
=> y = 4
Thay y = 4 vào ( 1 ) ta được :
4x + 7 x 4 = 16
=> 4x + 28 = 16
=> 4x = 16 - 28
=> 4x = - 12
=> x = - 3
Vậy x = - 3 ; y = 4
\(b,\hept{\begin{cases}3x+5y=1\\2x+y=-4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3x+5.\left(-4-2x\right)=1\\y=-4-2x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3x-20-10x=1\\y=-4-2x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-7x-20=1\\y=-4-2x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-7x=21\\y=-4-2x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=-3\\y=-4-2.\left(-3\right)\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=-3\\y=2\end{cases}}\)
28 tháng 2 2023
a: Vì m/1<>-m/1
neen hệ luôn có nghiệm
b: mx-y=2 và x+my=3
=>y=mx-2 và x+m(mx-2)=3
=>y=mx-2 và x(1+m^2)=5
=>x=5/m^2+1 và y=5m/m^2+1-2=(5m-2m^2-2)/m^2+1=(-2m^2+5m-2)/m^2+1
x>0; y>0
=>5>0 và -2m^2+5m-2>0
=>2m^2-5m+2<0
=>2m^2-4m-m+2<0
=>(m-2)(2m-1)<0
=>1/2<m<2
CM
11 tháng 12 2017
Ta có 2 x + 1 3 − y + 1 4 = 4 x − 2 y + 2 5 2 x − 3 4 − y − 4 3 = − 2 x + 2 y − 2
⇔ 40 x + 20 − 15 y − 15 = 48 x − 24 y + 24 6 x − 9 − 4 y + 16 = − 24 x + 24 y − 24
⇔ 8 x − 9 y = − 19 30 x − 28 y = − 31 ⇔ 120 x − 135 = − 285 120 x − 112 = − 124 ⇔ x = 11 2 y = 7
Thay x = 11 2 ; y = 7 vào phương trình 6mx – 5y = 2m – 66 ta được:
6m. 11 2 − 5.7 = 2m – 66 31m = −31 m = −1
Đáp án: A
CM
10 tháng 9 2017
Đáp án B
Phương pháp: Đặt t = 2 x
Cách giải: Đặt t = 2 x ta có:
Khi đó phương trình trở thành
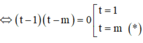
Để phương trình ban đầu có 3 nghiệm phân biệt 
có nghiệm 
16 tháng 2 2017
Câu 1 : \(a,\hept{\begin{cases}4x+7y=16\left(1\right)\\4x-3y=-24\left(2\right)\end{cases}}\)
Lấy ( 1 ) trừ ( 2 ) ta được :
10y = 40
=> y = 4
Thay y = 4 vào ( 1 ) ta được :
4x + 7 . 4 = 16
=> 4x + 28 = 16
=> 4x = 16 - 28
=> 4x = -12
=> x = - 3
Vậy x = - 3 ; y = 4
\(b,\hept{\begin{cases}3x+5y=1\\2x+y=-4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}6x+10y=2\left(1\right)\\6x+3y=-12\left(2\right)\end{cases}}\)
Lấy ( 1 ) trừ ( 2 ) ta được :
7y = 14
=> y = 2
Thay y = 2 vào ( 1 )
Ta được : 6x + 10 . 2 = 2
=> 6x + 20 = 2
=> 6x = 2 - 20
=> 6x = - 18
=> x= - 3
Vậy x = - 3 ; y = 2
