Tìm giá trị nhỏ nhất của biểu thức sau: M = 5x2 +y2 + 2x(y-2)+2021
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
8 tháng 8 2017
\(M=x^2+5y^2-4xy+2x-8y+2021\)
\(=\left(x^2-4xy+4y^2\right)+2\left(x-2y\right)+1+\left(y^2-4y+4\right)+2016\)
\(=\left(x-2y+1\right)^2+\left(y-2\right)^2+2016\ge2016\)
Vậy GTNN của M là 2016 đạt đươc tại \(\hept{\begin{cases}x=3\\y=2\end{cases}}\)
PV
1
16 tháng 11 2021
=4x2+4xy+y2+x2-6x-2y+1
=(2x+y)2-4x-2y+1+x2-2x+1-1
=[(2x+y)2-2(2x+y)+1]+(x-1)2-1
=(2x+y+1)2+(x-1)2-1
ta có: (2x+y+1)2\(\ge0\)với\(\forall\)x
(x-1)2\(\ge0\)với \(\forall\)x
\(\Rightarrow\left(2x+y+1\right)^2+\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(2x+y+1\right)^2+\left(x+1\right)^2-1\ge-1\forall x\)
\(\Rightarrow N\ge-1\)
Dấu '=' xảy ra\(\Leftrightarrow\hept{\begin{cases}\left(2x+y+1\right)^2=0\\\left(x-1\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}}\)
vậy N đạt GTNN là -1 khi và chỉ khi x=1;y=-3
25 tháng 7 2021
a, \(A=2x^2+11\ge11\)
Dấu ''='' xảy ra khi x = 0
Vậy GTNN A là 11 khi x = 0
b, \(B=\left(x-3\right)^2+2021\ge2021\)
Dấu ''='' xảy ra khi x = 3
Vậy GTNN B là 2021 khi x = 3
25 tháng 7 2021
a) Ta có: \(2x^2\ge0\forall x\)
\(\Leftrightarrow2x^2+11\ge11\forall x\)
Dấu '=' xảy ra khi x=0
b) Ta có: \(\left(x-3\right)^2\le0\forall x\)
\(\Leftrightarrow\left(x-3\right)^2+2021\ge2021\forall x\)
Dấu '=' xảy ra khi x-3=0
hay x=3
23 tháng 7 2021
a) Ta có: \(\left|x-2021\right|\ge0\forall x\)
\(\Leftrightarrow2\left|x-2021\right|\ge0\forall x\)
\(\Leftrightarrow2\left|x-2021\right|+9\ge9\forall x\)
Dấu '=' xảy ra khi x=2021
b) Ta có: \(\left|x-2\right|\ge0\forall x\)
\(\left|y+1\right|\ge0\forall y\)
Do đó: \(\left|x-2\right|+\left|y+1\right|\ge0\forall x,y\)
\(\Leftrightarrow\left|x-2\right|+\left|y+1\right|+2021\ge2021\forall x,y\)
Dấu '=' xảy ra khi (x,y)=(2;-1)
17 tháng 12 2021
a) \(M=2022-\left|x-9\right|\le2022\)
\(maxM=2022\Leftrightarrow x=9\)
b) \(N=\left|x-2021\right|+2022\ge2022\)
\(minN=2022\Leftrightarrow x=2021\)
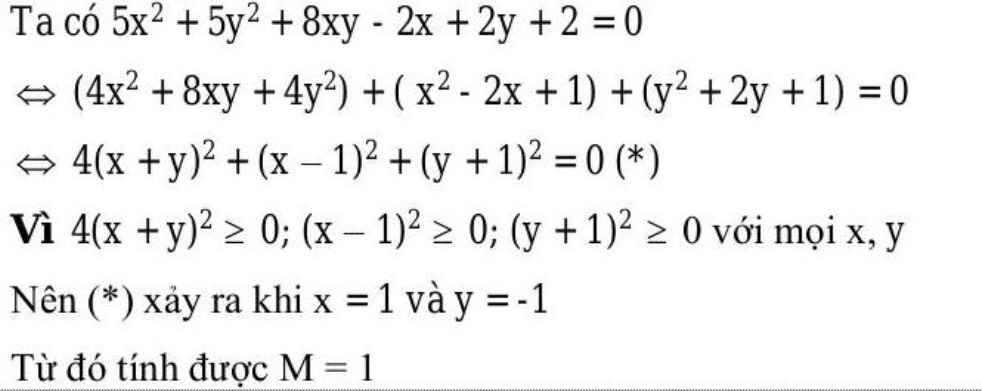
M=5x^2+y^2+2x(y-2)+2021
<=> M = 5x^2 + y^2 + 2xy - 4x + 2021
<=> M = 4x^2 + x^2 + y^2 + 2xy - 4x + 1 + 2020
<=> M = ( 4x^2 - 4x + 1) + (x^2 +2xy+y^2) +2020
<=> M =(2x-1)^2 + (x+y)^2 + 2020
Vì: (2x-1)^2 + (x+y)^2 > 0
=> (2x-1)^2 + (x+y)^2 + 2020 > 2020
Dấu "=" xảy ra khi và chỉ khi : (2x-1)^2=0 => 2x-1 = 0 => 2x= 1 => x=1/2
(x+y)^2=0 => x+y=0 => 1/2 + y =0 => y= 0- 1/2 => y=-1/2
Vậy Mmin = 2020 khi x=1/2;y=-1/2