0 < a < b , a + b = 42 và BCNN (a,b) = 72
Giúp tui với ! :((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BM
1
Những câu hỏi liên quan
HT
1
N
29 tháng 1 2023
a,
Ta có: 72 = 2 3 . 3 2 => Trong hai số có ít nhất 1 số chia hết cho 2
Giả sử a ⋮ 2 => b = (42 – a) ⋮ 2 (1)
Lập luận tương tự, ta có a ⋮ 3; b ⋮ 3 (2)
Từ (1), (2) => a ⋮ 6; b ⋮ 6
Ta có: 42 = 6+36 = 12+30 = 18+24
Trong các cặp trên chỉ có duy nhất (a;b) ∈ {(18;24),(24;18)} thỏa mãn đề bài
NN
1
16 tháng 10 2023
Vì BCLN(a;b)=72
Nên a;b ϵ Ư(72)
Liệt kê Ư(72)={1;2;3;4;6;8;9;12;18;24;36}
Vì a+b=42
Nên a=18;b=24
6 tháng 12 2023
Ta thấy \(72=2^3.3^2\) nên a, b có dạng \(\left\{{}\begin{matrix}a=2^x3^y\\b=2^z.3^t\end{matrix}\right.\) với \(x,y,z,t\inℕ\) và \(max\left\{x,z\right\}=3;max\left\{y,t\right\}=2\).
Theo đề bài, ta có \(2^x.3^y+2^z.3^t=42\)
\(\Leftrightarrow2^{x-1}.3^{y-1}+2^{z-1}3^{t-1}=7\) (*), do đó \(x,y,z,t\ge1\)
TH1: \(x\ge z,y\le t\). Khi đó \(x=3,t=2\). (*) thành:
\(4.3^{y-1}+3.2^{z-1}=7\) \(\Leftrightarrow y=z=1\)
Vậy \(\left\{{}\begin{matrix}a=24\\b=18\end{matrix}\right.\) (nhận)
TH2: KMTQ thì giả sử \(x\ge z,y\ge t\). Khi đó \(x=3,z=2\). (*) thành
\(4.3^{y-1}+2.3^{t-1}=7\), điều này là vô lí.
Vậy \(\left(a,b\right)=\left(24,18\right)\) hay \(\left(18,24\right)\) là cặp số duy nhất thỏa yêu cầu bài toán.
NP
1 tháng 12 2015
do 72=2^3.3^2.23.32
nên ít nhất trong 2 số a, b có một số chia hết cho 2
giả sử a chia hết cho 2 => b=42-a cũng chia hết cho 2
=> a và b đều chia hết cho 2.
tương tự ta cũng có a và b chia hết cho 3
=> a và b đều chia hết cho 6.
dễ thấy 42=36+6=30+12=18+24 (tổng 2 số chia hết cho 6)
trong 3 tổng trên chỉ có cặp 18 và 24 là thỏa mãn.
=> a=18 và b=24
TN
2 tháng 1 2016
Ta có:
72=32∗23
mà a,b là các số tự nhiên
=>a,b <42
Do 72 là BCNN
=>a = 9k(k<5)
b=8q(q<6)
=>a=18 và b=24
vậy tập nghiệm cua phương trình là
(a,b) =(24;18) và các hoán vị của nó
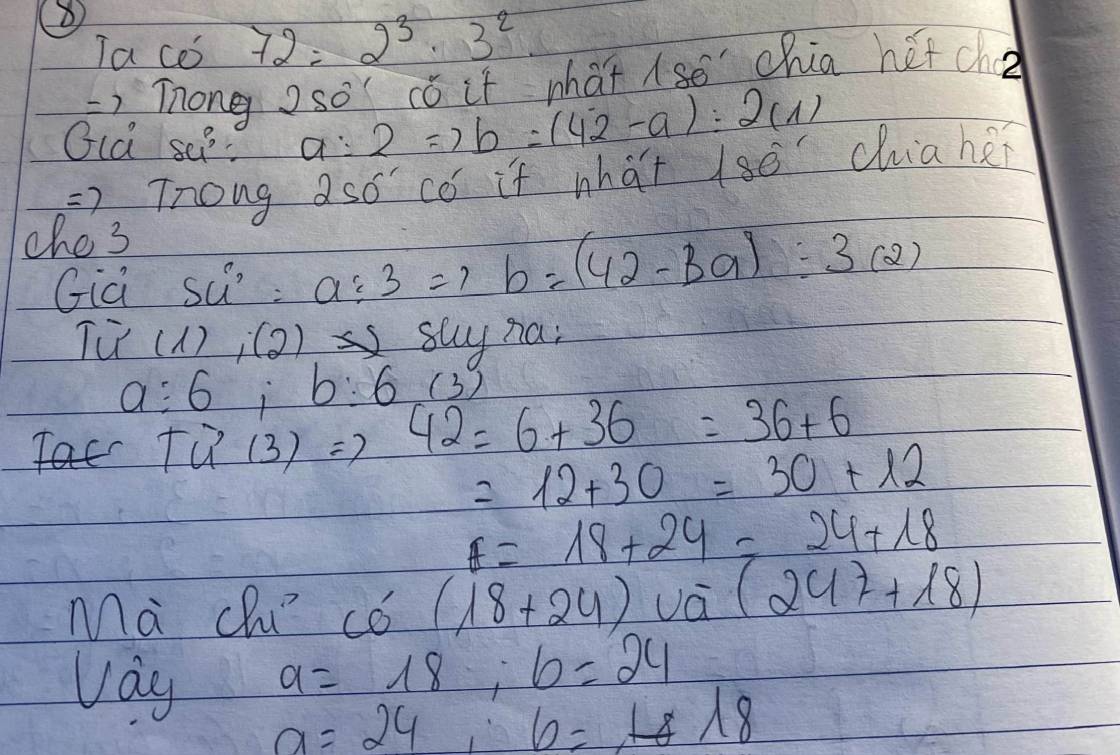
Giúp tui đi ;-;