Hệ phương trình
- (m+1)x-y=m+1
- x+(m-1)y=2
có nghiệm là x0;y0
Giá trị nhỏ nhất S= x0+y0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có
3 x − y = 2 m + 1 x + 2 y = − m + 2 ⇔ 6 x − 2 y = 4 m + 2 x + 2 y = − m + 2 ⇔ 7 x = 3 m + 4 x + 2 y = − m + 2 ⇔ x = 3 m + 4 7 3 m + 4 7 + 2 y = − m + 2 ⇔ x = 3 m + 4 7 2 y = − 7 m + 14 7 − 3 m + 4 7 ⇔ x = 3 m + 4 7 y = − 5 m + 5 7
hệ phương trình có nghiệm duy nhất ( x ; y ) = 3 m + 4 7 ; − 5 m + 5 7
Để x – y = 1 thì 3 m + 4 7 − − 5 m + 5 7 = 1 ⇔ 8m – 1 = 7 ⇔ 8m = 8 m = 1
Vậy với m = 1 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x − y = 1
Đáp án: C

Thay m = 1 vào hệ phương trình đã cho ta được:
x − y = 2 x + 2 y = 5 ⇔ 2 x − 2 y = 4 x + 2 y = 5 ⇔ 3 x = 9 x + 2 y = 5 ⇔ x = 3 y = 1
Vậy hệ phương trình đã cho có nghiệm duy nhất là (3; 1) khi m = 1
Đáp án: A

Thay m = 1 vào hệ phương trình đã cho ta được:
x − y = 2 x + 2 y = 5 ⇔ 2 x − 2 y = 4 x + 2 y = 5 ⇔ 3 x = 9 x + 2 y = 5 ⇔ x = 3 y = 1
Đáp án:A

Thay m = 2 vào hệ ta được x + y = 2 2 x + y = 3
Khi đó x + y = 2 2 x + y = 3 ⇔ x + y = 2 x = 1 ⇔ x = 1 y = 1
Vậy hệ phương trình có nghiệm duy nhất (1; 1) khi m = 2
Đáp án: D

Đáp án D
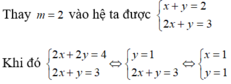
Vậy hệ phương trình có nghiệm duy nhất (1; 1) khi m = 2

Ta có
x + 1 4 − y 2 = x + y + 1 x − 2 2 + y − 1 3 = x + y − 1
⇔ x + 1 − 2 y = 4 x + 4 y + 4 3 x − 6 + 2 y − 2 = 6 x + 6 y − 6
⇔ 3 x + 6 y = − 3 3 x + 4 y = − 2 ⇔ y = − 1 2 x = 0
Thay x = 0; y = − 1 2 vào phương trình (m + 2)x + 7my = m – 225 ta được:
(m + 2).0 + 7m − 1 2 = m – 225 ⇔ 9 2 m = 225 ⇔ m = 50
Đáp án: C

Từ (m – 1) x + y = 2 thế vào phương trình còn lại ta được phương trình:
mx + 2 – (m – 1) x = m + 1 ⇔ x = m – 1 suy ra y = 2 – ( m – 1 ) 2 với mọi m
Vậy hệ phương trình luôn có nghiệm duy nhất ( x ; y ) = ( m – 1 ; 2 – ( m – 1 ) 2 )
2 x + y = 2 ( m – 1 ) + 2 – ( m – 1 ) 2 = − m 2 + 4 m – 1 = 3 – ( m – 2 ) 2 ≤ 3 với mọi m
Đáp án: A