cho tam giác MNP vuông tại M. Trên MN lấy một điểm Q, vẽ đường tròn đường kính NQ và cắt NP tại E. kế đường thẳng PQ cắt đường tròn tại D
a/ Vẽ hình
b/ Chứng minh : tứ giác MPND nội tiếp
c/ Chứng minh : góc DMN = goc DPN
d/ Chứng minh : MN là đường phân giác của góc DME

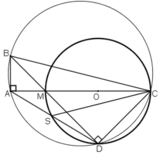
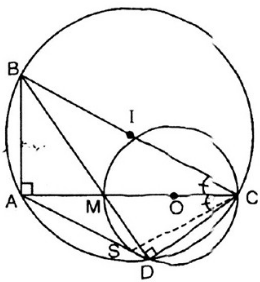
 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
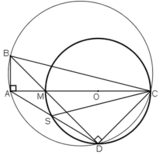
 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
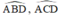 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 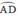
 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 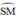
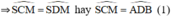
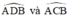 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 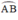
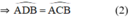


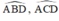 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 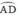
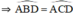
b/ Xét tứ giác MPND có:
góc NMP =90 độ (do tam giác MNP vuông tại M)(1)
Tam giác NDQ nội tiếp đường tròn đường kính NQ có cạnh NQ là đường kính
=> tam giác NDQ vuông tại D
=> góc QDN =90 độ(2)
Từ (1) và (2)=> góc QDN = gócNMP
=> tứ giác MPND nội tiếp (đpcm)
c/Từ giác MPND nội tiếp (c/m câu b)
=> góc DMN=góc DPN (cùng chắn cungDN) (đpcm)
d/Xét tứ giác MQEP có:
góc QMP=90 độ (do tam giác MNP vuông tại M và M, Q,N thẳng hàng) (3)
Tam giác NQE nội tiếp đường tròn đường kính NQ có cạnh NQ là đường kính
=> tam giác NQE vuông tại E
=> góc NEQ=90 độ
=> góc QEP=90 độ (góc NEQ+góc QEP=90 độ do kề bù) (4)
Từ (3) và (4)=> tứ giác MQEP nội tiếp
=> góc QME=gócQPE
hay góc NME=góc DPN (do D,Q,P thẳng hàng và N,Q,M thẳng hàng) (5)
Mà góc DPN=góc DMN (c/m câu c) (6)
từ (5) và (6)=> góc DMN=góc NME (7)
Mặt khác: tia MN nằm giữa 2 tia MD và ME (8)
Từ (7) và (8)=> MN là đường phân giác của góc DME (đpcm)