Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD
b: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là tia phân giác của góc BAC
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là đường cao
=>AD⊥BC
mà d//BC
nên AD⊥d
a) Xét ΔΔABD và ΔΔACD có:
AB = AC (gt)
AD: cạnh chung
BD = CD (D là trung điểm của BC)
⇒Δ⇒ΔABD = ΔΔACD (c.c.c)
b)b) Ta có: ΔΔABD = ΔΔACD (theo ý a)
⇒\(\widehat{BAD}\)=\(\widehat{CAD}\) (2gocs tương ứng )
⇒ AD là tia phân giác của \(\widehat{BAC}\)
c) Ta có: ΔΔABD = ΔΔACD (theo ý a)
⇒ \(\widehat{ADB}\)=\(\widehat{ADC}\)(2 góc tương ứng )
mà \(\widehat{ADB}\) + \(\widehat{ADC}\)=18001800( 2 góc kề bù )
⇒\(\widehat{ADB}\)=\(\widehat{ADC}\)= 900900
⇒ AD ⊥ BC
Lại có: d // BC (gt) ⇒ AD ⊥ d
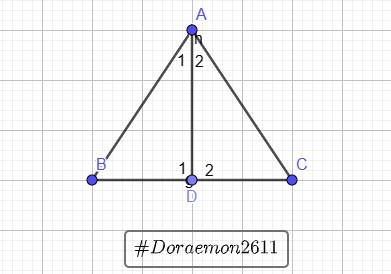
`a)` Vì `D` là trung điểm `BC=>DB=DC`
Xét `\triangle ABD` và `\triangle ACD` có:
`{:(AB=AC),(AD\text{ là cạnh chung}),(BD=CD):}}=>\triangle ABD=\triangle ACD` (c-c-c)
`b)` Vì `D` là tđ của `BC=>AD` là đường trung tuyến trong `\triangle ABC` cân tại `A`
`=>AD` đồng thời là đường phân giác của `\triangle ABC`
`=>AD` là tia phân giác của `\hat{BAC}`
`c)` Vì `D` là tđ của `BC=>AD` là đường trung tuyến trong `\triangle ABC` cân tại `A`
`=>AD` đồng thời là đường cao của `\triangle ABC`
`=>AD \bot BC`
`a,` Xét Tam giác `ABD` và Tam giác `ACD` có (bạn lưu ý ghi đúng tên của Tam giác để có các cạnh và góc tương ứng nhé)
`AB = AC (g``t)`
AD chung
`DB = DC (g``t)`
`=>` Tam giác `ABD =` Tam giác `ACD (c-c-c)`
`b,` Vì Tam giác `ABD =` Tam giác `ACD (a)`
`=>` \(\widehat{BAD}=\widehat{CAD}\) (2 góc tương ứng)
`=> AD` là tia phân giác của \(\widehat{BAC}\)
`c,` Vì Tam giác `ABD =` Tam giác `ACD (a)`
`=>` \(\widehat{ADB}=\widehat{ADC}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí kề bù
`=>`\(\widehat{ADB}+\widehat{ADC}=180^0\)
`=>` \(\widehat{ADB}=\widehat{ADC}=\) \(\dfrac{180}{2}=90^0\)
`=>`\(AD\perp BC\) `(đpcm)`
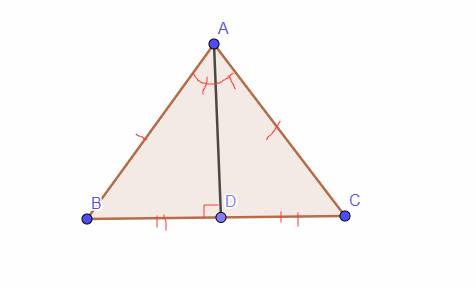
a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
b: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của \(\widehat{BAC}\)
c: ΔABD=ΔACD
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD\(\perp\)BC
a) Xét \(\Delta\)ABD và \(\Delta\)ACD có:
AB = AC (gt)
AD: cạnh chung
BD = CD (D là trung điểm của BC)
\(\Rightarrow\Delta\)ABD = \(\Delta\)ACD (c.c.c)
b) Ta có: \(\Delta\)ABD = \(\Delta\)ACD (theo ý a)
\(\Rightarrow\widehat{BAD}\) = \(\widehat{CAD}\) (2 góc tương ứng)
\(\Rightarrow\) AD là tia phân giác của \(\widehat{BAC}\)
c) Ta có: \(\Delta\)ABD = \(\Delta\)ACD (theo ý a)
\(\Rightarrow\widehat{ADB}\) =\(\widehat{ADC}\) (2 góc tương ứng)
mà \(\widehat{ADB}\) + \(\widehat{ADC}\) = 18001800 (2 góc kề bù)
\(\Rightarrow\widehat{ADB}\) = \(\widehat{ADC}\) = 900900
\(\Rightarrow\) AD \(\perp\) BC
Lại có: d // BC (gt) \(\Rightarrow\) AD \(\perp\) d
ĐS:......................
#Châu's ngốc
