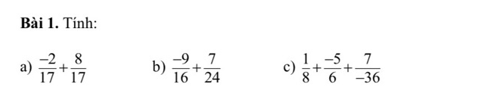Giusp mik đi ak!
Giusp mik đi ak!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
VT: \(\left(a+b\right)^2=\left(a+b\right)\left(a+b\right)\)
\(=a^2-ab-ab+b^2=a^2-2ab+b^2=VP\)
\(\Rightarrow\left(a+b\right)^2=a^2-2ab+b^2\left(đpcm\right)\)
hok tốt!!

f: =>(x-3)(x-1)>=0
=>x>=3 hoặc x<=1
g: =>(x-2)(x^2+3)<0
=>x-2<0
=>x<2
h: =>x+2>=0
=>x>=-2
i: =>(x-1-x+3)/(x-3)>0
=>x-3>0
=>x>3


a)\(\dfrac{-2}{17}+\dfrac{8}{17}=\dfrac{6}{17}\)
b) \(\dfrac{-9}{16}+\dfrac{7}{24}=\dfrac{-13}{48}\)
c)\(\dfrac{1}{8}+\dfrac{-5}{6}+\dfrac{7}{-36}=\dfrac{-17}{24}+\dfrac{7}{-36}=\dfrac{-65}{72}\)
a) =\(\dfrac{-2+8}{17}=\dfrac{6}{17}\)
b) =\(\dfrac{-27}{48}+\dfrac{14}{48}=\dfrac{-27+14}{48}=\dfrac{-13}{48}\)
c) \(=\dfrac{9}{72}+\dfrac{-60}{72}+\dfrac{-14}{72}=\dfrac{9+\left(-60\right)+\left(-14\right)}{72}=\dfrac{-65}{72}\)



Lời giải:
Ta có:
\(P=1+x+x^2+x^3+...+x^9+x^{10}\)
\(\Rightarrow xP=x+x^2+x^3+...+x^{10}+x^{11}\)
Trừ theo vế:
\(xP-P=(x+x^2+x^3+...+x^{10}+x^{11})-(1+x+x^2+...+x^{10})\)
\(\Rightarrow \)\(xP-P=x^{11}-1\) (đpcm)
P.s: Bạn lưu ý lần sau nhớ viết công thức rõ ràng.