Cho đẳng thức sau: 𝑥. 𝑦 = −2.3. Tỉ lệ thức nào đúng khi được suy ra từ đẳng thức đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\dfrac{2}{4}=\dfrac{3}{6};\dfrac{6}{4}=\dfrac{3}{2};\dfrac{2}{3}=\dfrac{4}{6};\dfrac{4}{3}=\dfrac{4}{2}\\ b,\text{Đặt }\dfrac{x}{4}=\dfrac{y}{7}=k\Rightarrow x=4k;y=7k\\ \text{Ta có }xy=112\\ \Rightarrow28k^2=112\\ \Rightarrow k^2=4\Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=8;y=14\\x=-8;y=-14\end{matrix}\right.\)

từ tỉ lệ thức
\(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)
có thể suy ra được tỉ lệ thức
a:b=c:d

\(\dfrac{x}{y}=\dfrac{y}{z}=\dfrac{z}{t}=\dfrac{t}{x}=\dfrac{x+y+z+t}{y+z+t+x}=1\\ \Rightarrow\left\{{}\begin{matrix}x=y\\y=z\\z=t\\t=x\end{matrix}\right.\Rightarrow x=y=z=t\\ \Rightarrow M=\dfrac{2x-x}{x+x}+\dfrac{2x-x}{x+x}+\dfrac{2x-x}{x+x}+\dfrac{2x-x}{x+x}=\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=2\)

Câu 1: D
Câu 2: C
Câu 3:
\(\sqrt{\dfrac{9}{49}}=\sqrt{\left(\dfrac{3}{7}\right)^2}=\dfrac{3}{7}\) là số hữu tỉ
\(\sqrt{49}=7\) là số hữu tỉ
\(\sqrt{0,9}=\sqrt{\dfrac{9}{10}}=\dfrac{3}{\sqrt{10}}\) là số vô tỉ
\(\sqrt{0,03}\) là số vô tỉ
=>Trong các số này có hai số là số vô tỉ đó là \(\sqrt{0,9};\sqrt{0,03}\)

\(7,\\ a,A=x^2-4x+3+11=\left(x-2\right)^2+10\ge10\\ \text{Dấu }"="\Leftrightarrow x=2\\ b,B=-\left(4x^2-4x+1\right)+6=-\left(2x-1\right)^2+6\le6\\ \text{Dấu }"="\Leftrightarrow x=\dfrac{1}{2}\\ c,x-y=2\Leftrightarrow x=y+2\\ \Leftrightarrow B=y^2-3x^2=y^2-3\left(y+2\right)^2\\ \Leftrightarrow B=y^2-3y^2-12y-12=-4y^2-12y-12\\ \Leftrightarrow B=-\left(4y^2+12y+9\right)-3=-\left(2y+3\right)^2-3\le-3\\ \text{Dấu }"="\Leftrightarrow y=-\dfrac{3}{2}\Leftrightarrow x=\dfrac{1}{2}\)
\(8,\\ \Leftrightarrow x^3-3x^2+5x+a=\left(x-2\right)\cdot a\left(x\right)\)
Thay \(x=2\Leftrightarrow8-12+10+a=0\Leftrightarrow a=-6\)
 có thể suy ra được tỉ lệ thức nào
có thể suy ra được tỉ lệ thức nào . Tỉ lệ thức được suy ra từ đẳng thức là:
. Tỉ lệ thức được suy ra từ đẳng thức là: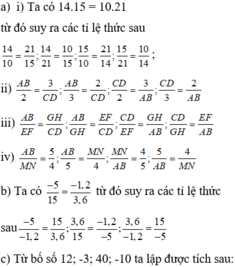
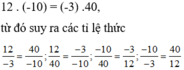
Đề thiếu rồi bạn