Question

[Nguyễn Hà Thục Nhi]

A= 1/2^2+1/3^2+1/4^2+...+1/2002^2. Chứng tỏ A không phải là số tự nhiên. 

Answer 1

[Akai Haruma]

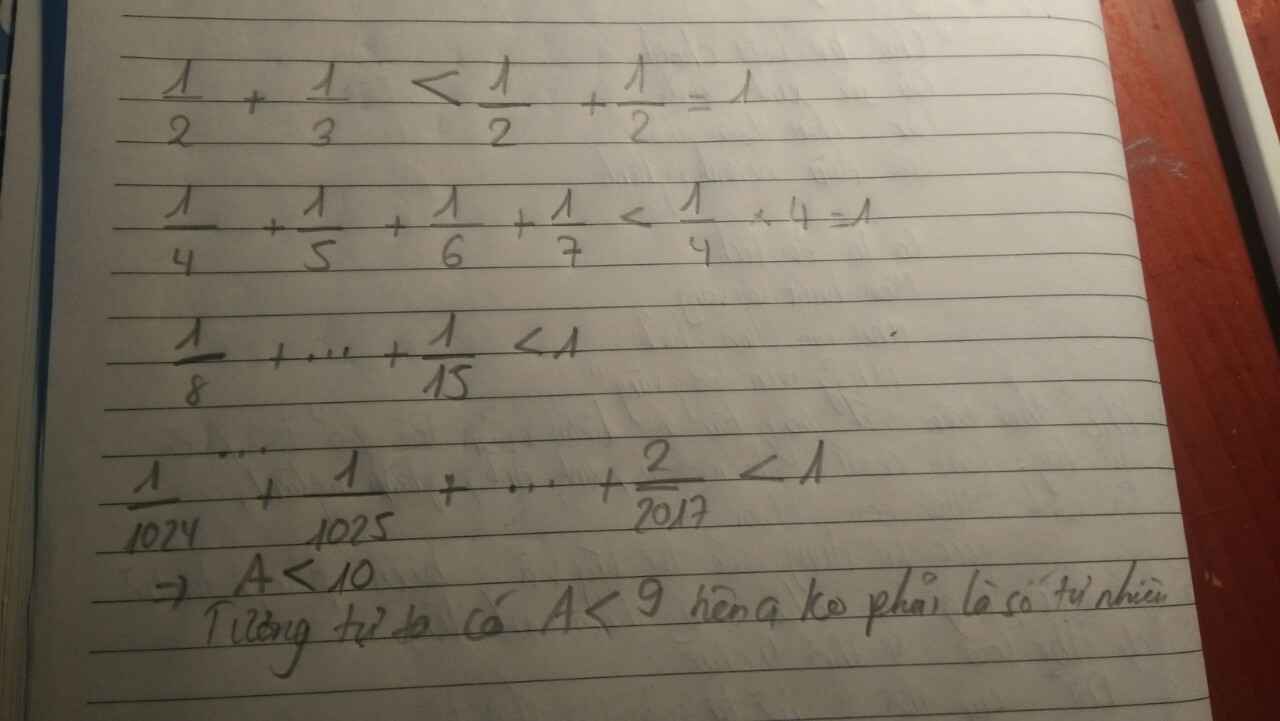
Lời giải:

$A<\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2001.2002}$

$=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+...+\frac{2002-2001}{2001.2002}$

$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{2001}-\frac{1}{2002}$
$=1-\frac{1}{2002}<1$

Mà hiển nhiên $A>0$

$\Rightarrow 0< A< 1$. Do đó $A$ không phải số tự nhiên.