So sánh hai số sau: (-2)^100 và (-4)^50
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CC
5
9 tháng 7 2018
a) ta có: \(2^{100}=\left(2^2\right)^{50}=4^{50}\) và 550
Vì 4 < 5 => 450 < 550
Vậy 2100 < 550
b) Ta có: \(4^{30}=\left(4^3\right)^{10}=64^{10}\)
\(8^{20}=\left(8^2\right)^{10}=64^{10}\)
Vì 64 = 64 => 6410 = 6410
Vậy 430 = 820
LT
3
HP
2
5 tháng 3 2022
\(\dfrac{99}{100}=1-\dfrac{1}{100}\)
\(\dfrac{100}{99}=1+\dfrac{1}{99}\)
\(\dfrac{100}{99}>\dfrac{99}{100}\)
xin TICH. chúc bạn học tốt
24 tháng 6 2020
\(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{50^2}\)
Ta có : \(\frac{1}{2^2}=\frac{1}{2\cdot2}< \frac{1}{1\cdot2}\)
\(\frac{1}{3^2}=\frac{1}{3\cdot3}< \frac{1}{2\cdot3}\)
\(\frac{1}{4^2}=\frac{1}{4\cdot4}< \frac{1}{3\cdot4}\)
\(...\)
\(\frac{1}{50^2}=\frac{1}{50\cdot50}< \frac{1}{49\cdot50}\)
=> \(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{50^2}< \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{49\cdot50}\)
=> \(A< \frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{49}-\frac{1}{50}\)
=> \(A< 1-\frac{1}{50}=\frac{49}{50}\)( 1 )
Lại có : \(\frac{49}{50}< 1\)( 2 )
Từ ( 1 ) và ( 2 ) => \(A< \frac{49}{50}< 1\)
=> \(A< 1\)
16 tháng 6 2016
50 số chẵn nguyên dương đầu tiên có trung bình cộng là : 1/2(2+100) = 51
50 số lẻ nguyên dương đầu tiên có trung bình cộng là : 1/2(1+99) = 50
Vậy, tổng chẵn > tổng lẻ.
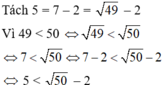
\(\left(-2\right)^{100}=2^{100}=\left(2^2\right)^{50}=4^{50}=\left(-4\right)^{50}\)
bn MAnh hc giỏi chăm chỉ quá :3