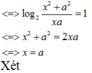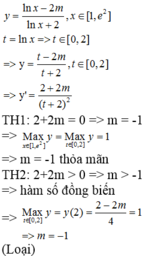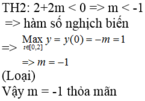Số các giá trị của n thỏa mãn 2n-1 là ước của 25 là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1D
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
10 tháng 5 2022
n+4 là ước của 2n+3 \(\Rightarrow2n+3⋮n+4\)
\(\dfrac{2n+3}{n+4}=\dfrac{2n+8-5}{n+4}=\dfrac{2\left(n+4\right)-5}{n+4}=2-\dfrac{5}{n+4}\)
=> n+4 phải là ước của 5
\(\Rightarrow n+4=\left\{-5;-1;1;5\right\}\Rightarrow n=\left\{-9;-5;-3;1\right\}\)
DT
0
CM
13 tháng 9 2018
Chọn B
Cách giải: Ta có:
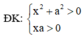
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
TN
19 tháng 12 2015
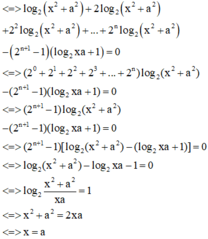
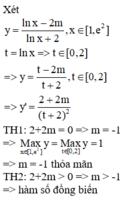
Trong một số trường hợp, có thể sử dụng mối quan hệ đặc biệt giữa ƯCLN, BCNN và tích của hai số nguyên dương a, b, đó là : ab = (a, b).[a, b], trong đó (a, b) là ƯCLN và [a, b] là BCNN của a và b. Việc chứng minh hệ thức này khụng khú :
Theo định nghĩa ƯCLN, gọi d = (a, b) => a = md ; b = nd với m, n thuộc Z+ ; (m, n) = 1 (*)
Từ (*) => ab = mnd2 ; [a, b] = mnd
=> (a, b).[a, b] = d.(mnd) = mnd2 = ab
=> ab = (a, b).[a, b] . (**)