giải chi tiết hộ nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc yOz=180-60=120 độ
góc zOm=góc yOm=120/2=60 độ
b: góc xOn=góc zOm=60 độ
=>góc xOn=góc xOy
=>Ox là phân giác của góc yOn

1: \(=\dfrac{1}{7}+\dfrac{3}{4}-\dfrac{8}{7}=\dfrac{3}{4}-1=-\dfrac{1}{4}\)



hình như tui vừa hỏi câu này xong nhưng người giải bài này hơi ẩu:)) hóng đáp án tui chép chung với kkk

Lời giải:
a.
Tại $x=5$ thì $B=\frac{5+3}{5-2}=\frac{8}{3}$
b.
\(A=\frac{x^2-x+1}{(x-2)(x+2)}+\frac{2(x+2)}{(x-2)(x+2)}-\frac{x-2}{(x-2)(x+2)}=\frac{x^2-x+1+2(x+2)-(x-2)}{(x-2)(x+2)}\)
\(=\frac{x^2+7}{(x-2)(x+2)}\)
c.
\(P=A:B(x+2)=\frac{x^2+7}{(x-2)(x+2)}:\frac{x+3}{x-2}.(x+2)=\frac{x^2+7}{x+3}\)
Áp dụng BĐT Cô-si:
$x^2+1\geq 2|x|\geq 2x$
$\Rightarrow x^2+7\geq 2x+6=2(x+3)$
$\Rightarrow P\geq \frac{2(x+3)}{x+3}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $x^2=1\Leftrightarrow x=\pm 1$ (tm)


 Giải chi tiết hộ mình nha!!!
Giải chi tiết hộ mình nha!!!
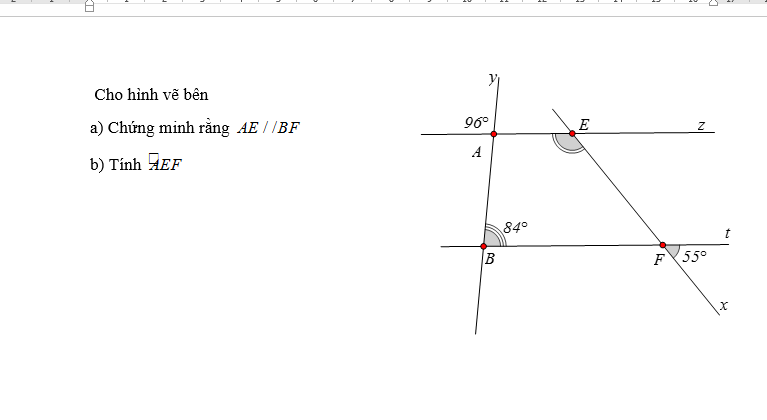
 Các bạn giải chi tiết hộ mình nha!
Các bạn giải chi tiết hộ mình nha!
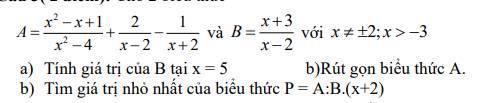
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{20}=\dfrac{2x-3y+z}{2\cdot9-3\cdot12+20}=\dfrac{6}{2}=3\)
Do đó: x=27; y=36; z=60
\(\dfrac{x}{3}\) = \(\dfrac{y}{4}\) ⇒ \(\dfrac{x}{3.3}\) = \(\dfrac{y}{3.4}\) = \(\dfrac{z}{5.4}\) = \(\dfrac{2x}{2.3.3}\) = \(\dfrac{3y}{3.3.4}\) = \(\dfrac{z}{5.4}\) ⇒ \(\dfrac{2x}{18}\) = \(\dfrac{3y}{36}\) = \(\dfrac{z}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{2x}{18}\) = \(\dfrac{3y}{36}\) = \(\dfrac{z}{20}\) = \(\dfrac{2x-3y+z}{18-36+20}\) = \(\dfrac{6}{2}\) = 3
\(x=\) 3 : \(\dfrac{2}{18}\) = 27; y = 3 : \(\dfrac{3}{36}\) = 36; z = 3 x 20 = 60
Vậy ..