CÂU 10: Cho tứ giác ABCD, và AC = BD ; Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất. a) c/m MNPQ là hình thôi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


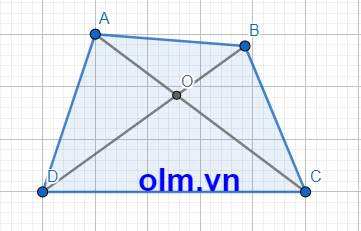
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)

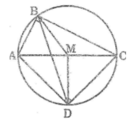
Trong đường tròn tâm M ta có BD là dây cung không đi qua tâm, AC là đường kính nên: BD < AC
AC = BD khi và chỉ khi BD là đường kính. Khi đó tứ giác ABCD là hình chữ nhật.

Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC, OCD và ODA.


Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
DO đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔBAD
Suy ra: MQ=BD/2=AC/2(3)
Từ (1), (2) và (3) suy ra MNPQ là hình thoi
Xét tam giác ABD có:
M là trung điểm của AB (gt).
Q là trung điểm của DA (gt).
=> MQ là đường trung bình.
=> 2MQ = BD (Tính chất đường trung bình). (1)
Xét tam giác ABC có:
M là trung điểm của AB (gt).
N là trung điểm của BC (gt).
=> MN là đường trung bình.
=> 2MN = AC (Tính chất đường trung bình). (2)
Xét tam giác ADC có:
Q là trung điểm của DA (gt).
P là trung điểm DC (gt).
=> PQ là đường trung bình.
=> 2PQ = AC (Tính chất đường trung bình) (3)
Xét tam giác BCD có:
N là trung điểm của BC (gt).
P là trung điểm của DC (gt).
=> PN là đường trung bình.
=> 2PN = BD (Tính chất đường trung bình). (4)
Lại có: AC = BD (gt). (5)
Từ (1) (2) (3) (4) (5) => MN = NP = PQ = MQ.
=> MNPQ là hình thoi.