\(\frac{1}{1-x}+\frac{2x}{x^2-1}=?\) MÌNH CẦN GẤP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
13 tháng 7 2019
a) \(\frac{x-1}{6}=\frac{2x+3}{7}\)
\(\Leftrightarrow7\left(x-1\right)=6\left(2x+3\right)\)
\(\Leftrightarrow7x-7=12x+18\)
\(\Leftrightarrow5x+18=-7\)
\(\Leftrightarrow5x=-25\)
\(\Leftrightarrow x=-5\)
KN
13 tháng 7 2019
b) \(\left(2x^2-\frac{1}{2}x\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow x\left(2x-\frac{1}{2}\right)\left(x^2+1\right)=0\)
Vì \(x^2+1>0\)nên \(\orbr{\begin{cases}x=0\\2x-\frac{1}{2}=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{1}{4}\end{cases}}\)
15 tháng 4 2020
Điều kiện xác định x khác 1
\(\frac{1}{x-1}-\frac{3x^2}{x^3-1}=\frac{2x}{x^2+x+1}\)
\(\Leftrightarrow\frac{1.\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{3x^2}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\Leftrightarrow x^2+x+1-3x^2=2x^2-2x\)
\(\Leftrightarrow x^2-3x^2-2x^2+x+2x+1=0\)
\(\Leftrightarrow-4x^2+2x+1=0\)
\(\Leftrightarrow\left(-2x-1\right)^2=0\)
\(\Leftrightarrow-2x-1=0\)
\(\Rightarrow x=-0,5\)(thỏa mãn)
S
14 tháng 12 2018
\(\frac{1}{x}-\frac{1}{x+1}=\frac{x+1-x}{x\left(x+1\right)}=\frac{1}{x^2+x}\)
b, \(\frac{1}{xy-x^2}-\frac{1}{y^2-xy}=\frac{y^2-xy-xy+x^2}{\left(xy-x^2\right)\left(y^2-xy\right)}=\frac{x^2+y^2}{xy^3-xyxy-xyxy+x^3y}\)Tu rut gon tiep
c, tt
d, cx r
14 tháng 12 2018
a) \(\frac{1}{x}-\frac{1}{x+1}=\frac{x+1}{x\left(x+1\right)}-\frac{x}{x\left(x+1\right)}\)
\(=\frac{x+1-x}{x\left(x+1\right)}=\frac{1}{x\left(x+1\right)}\)
b) \(\frac{1}{xy-x^2}-\frac{1}{y^2-xy}=\frac{1}{x\left(y-x\right)}-\frac{1}{y\left(y-x\right)}\)
\(=\frac{y}{xy\left(y-x\right)}-\frac{x}{xy\left(y-x\right)}=\frac{y-x}{xy\left(y-x\right)}=\frac{1}{xy}\)
c) \(\frac{9x-3}{4x-1}-\frac{3x}{1-4x}=\frac{9x-3}{4x-1}+\frac{3x}{4x-1}\)
\(=\frac{9x-3+3x}{4x-1}=\frac{6x-3}{4x-1}\)
21 tháng 9 2019
a) \(\frac{2x}{x+2}+\frac{x+2}{2x}=2\)
\(\Leftrightarrow4x^2+\left(x+2\right)^2=4x\left(x+2\right)\)
\(\Leftrightarrow5x^2+4x+4=4x^2+8x\)
\(\Leftrightarrow5x^2+4x+4-4x^2-8x=0\)
\(\Leftrightarrow x^2-4x+4=0\)
\(\Leftrightarrow x^2-2.x.2+2^2=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
\(\Rightarrow x=2\)
19 tháng 7 2021
c) Ta có: \(\left\{{}\begin{matrix}\dfrac{x+2}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x+1}+\dfrac{10}{y-2}=25\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{y-2}=22\\\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-2=\dfrac{1}{2}\\\dfrac{1}{x+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=1\\y-2=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{5}{2}\end{matrix}\right.\)
5 tháng 7 2017
a/ ĐK x-1 khác 0 ; x^2+x khác 0 ; x^3-x khác 0 ; 1-x^2 khác 0
=> x khác {1;0;-1}
b/ \(B=\frac{1}{x-1}-\frac{x^3-x}{x^2+x}.\left(\frac{1}{x^2-2x+1}+\frac{1}{1-x^2}\right)\)
\(=\frac{1}{x-1}-\frac{x\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}.\left(\frac{1}{\left(x-1\right)^2}+\frac{1}{\left(1+x\right)\left(1-x\right)}\right)\)
\(=\frac{1}{x-1}-\left(x-1\right).\left(\frac{1+x-x+1}{\left(x-1\right)^2\left(1+x\right)}\right)=\frac{1}{x-1}-\frac{1}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{x+1-1}{\left(x-1\right)\left(x+1\right)}=\frac{x}{x^2-1}\)
5 tháng 3 2022
c: \(=\dfrac{1}{3x-2}-\dfrac{4}{3x+2}+\dfrac{3x-6}{\left(3x-2\right)\left(3x+2\right)}\)
\(=\dfrac{3x+2-12x+8+3x-6}{\left(3x-2\right)\left(3x+2\right)}\)
\(=\dfrac{-6x+4}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{-2}{3x+2}\)
d: \(=\dfrac{x^2-4-x^2+10}{x+2}=\dfrac{6}{x+2}\)
e: \(=\dfrac{1}{2\left(x-y\right)}-\dfrac{1}{2\left(x+y\right)}-\dfrac{y}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x+y-x+y-2y}{2\left(x-y\right)\left(x+y\right)}=\dfrac{0}{2\left(x-y\right)\left(x+y\right)}=0\)
21 tháng 11 2017
\(A=\frac{2x+1}{x^2+2}=\frac{\left(x^2+2\right)-\left(x^2-2x+1\right)}{x^2+2}\)
\(=1-\frac{\left(x-1\right)^2}{x^2+2}\le1\forall x\)
DẤU "=" XẢY RA KHI X=1(ĐỀ LÀ TÌM MIN HOẶC MAX ĐÚNG KO BN)
\(B=\frac{4x+3}{x^2+1}=\frac{\left(x^2+4x+4\right)-\left(x^2+1\right)}{x^2+1}\)
\(=\frac{\left(x+2\right)^2}{x^2+1}-1\ge-1\forall x\)
DẤU "=" XẢY RA KHI X=-2
MÌNH LÀM HƠI TẮT BN THÔNG CẢM NHA
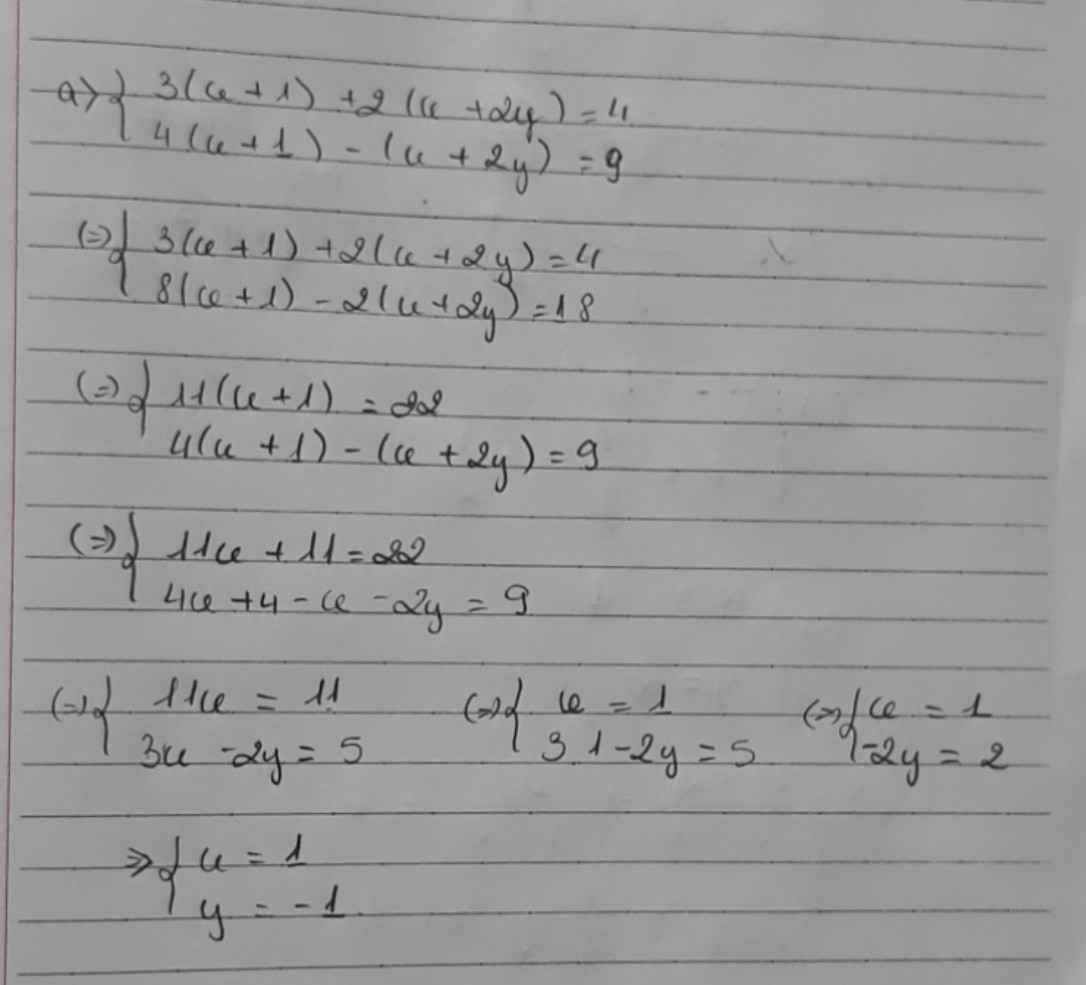
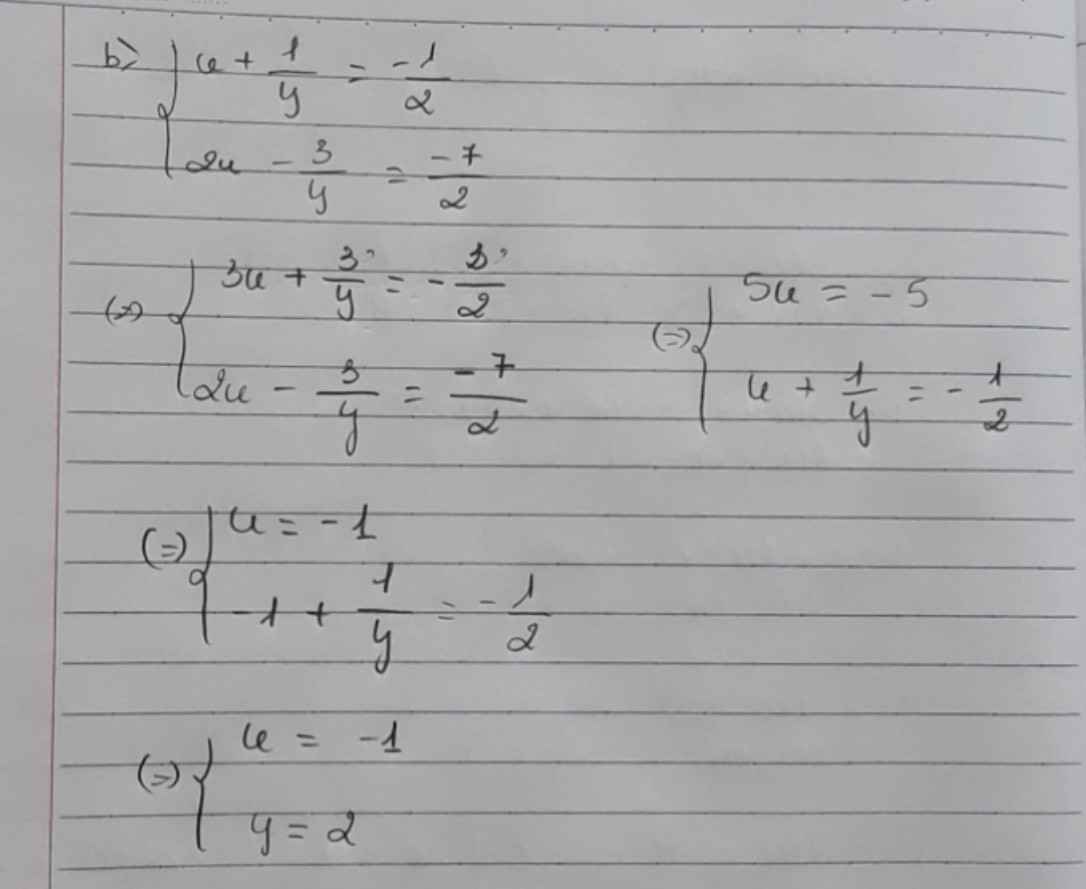
\(\frac{1}{1-x}+\frac{2x}{x^2+1}\)
\(\text{MTC:}\left(x-1\right)\left(x+1\right)\)
\(\frac{1}{1-x}=\frac{-1}{x-1}=\frac{-1.\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{-x-1}{\left(x-1\right)\left(x+1\right)}\)
\(\frac{2x}{x^2-1}=\frac{2x}{\left(x-1\right)\left(x+1\right)}\)
\(\frac{-1}{x-1}+\frac{2x}{x^2-1}=\frac{\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\frac{2x}{\left(x-1\right)\left(x+1\right)}=\frac{-x+1+2x}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{1}{x-1}\)
\(\text{Hok tốt!}\)
\(\text{@Kaito Kid}\)
Có gì sai cho em xin lỗi,tại mới học lớp 7;(((