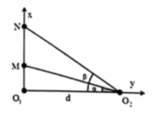
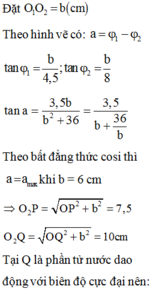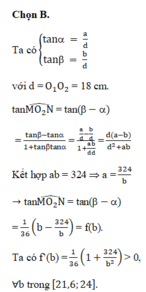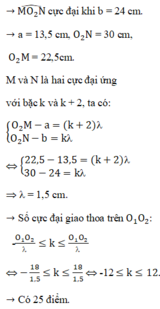Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp O1 và O2 dao động cùng pha, cùng biên độ. Chọn hệ tọa độ vuông góc Oxy (thuộc mặt nước) với gốc tọa độ là vị trí đặt nguồn O1 còn nguồn O2 nằm trên trục Oy. Hai điểm P và Q nằm trên Ox có OP = 4,5 cm và OQ = 8cm. Dịch chuyển nguồn O2 trên trục Oy đến vị trí sao cho góc \(PO_2Q\) có giá trị lớn nhất thì phần tử nước tại P không dao động còn phần tử nước tại Q dao động với biên độ cực đại. Biết giữa P và Q không còn cực đại nào khác. Trên đoạn OP, điểm gần P nhất mà các phần tử nước dao động với biên độ cực đại cách P một đoạn là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
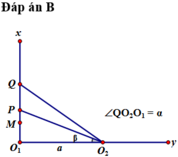
Đặt O1O2 = b (cm)
Theo hình vẽ ta có: a = φ 1 - φ 2
tan φ 1 = b 4 , 5 ; tan φ 2 = b 8 v à tan a = 3 , 5 b b 2 + 36 = 3 , 5 b + 36 b
Theo bất đẳng thức cosi thì a = amax khi b = 6 cm
Suy ra:
O 2 P = OP 2 + b 2 = 7 , 5 cm .
O 2 Q = OQ 2 + b 2 = 10 cm .
Tại Q là phần tử nước dao động với biên độ cực đại nên:
O 2 Q - OQ = kλ = 10 - 8 = 2 cm .
Tại P là phần tử nước không dao động nên P thuộc cực tiểu bậc k’
O 2 P - OP = ( k - 0 , 5 ) λ = 7 , 5 - 4 , 5 = 3 cm
với k’ = k + 1 (do giữa P và Q không còn cực đại nào)
kλ = 2 cm , ( k + 0 , 5 ) λ = 3 cm ⇒ λ = 2 cm , k = 1
Q là cực đại ứng với k = 1 nên cực đại M gần P nhất ứng với k = 2
O2M – OM = 4cm. Mặt khác O2M2 – OM2 = b2 = 36
O2M + OM = 36/4 = 9cm => 2OM = 5cm hay OM = 2,5cm
Do dó: MP = 5,5 – 2,5 = 2 cm.

- Đặt O1O2 = b (cm) . Theo hình vẽ ta có :
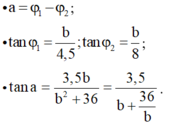
- Theo bất đẳng thức cosi thì a = amax khi b = 6 cm. Suy ra:
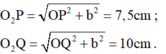
- Tại Q là phần tử nước dao động với biên độ cực đại nên:
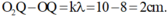
- Tại P là phần tử nước không dao động nên P thuộc cực tiểu bậc k’:
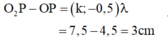
với k’ = k + 1 (do giữa P và Q không còn cực đại nào)
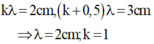
Q là cực đại ứng với k = 1 nên cực đại M gần P nhất ứng với k = 2
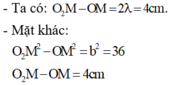
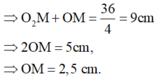
- Do đó: MP = 5,5 – 2,5 = 2 cm.


P O 2 - P O 1 = k + 0 ٫ 5 λ Q O 2 - Q O 1 = k λ ⇒ k + 0 ٫ 5 λ = 3 k λ = 2 ⇒ λ = 2 c m

Đáp án B
Đặt
![]()
Theo hình vẽ ta có :
![]()
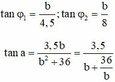
Theo bất đẳng thức cosi thì a=a max khi b = 6 cm
Suy ra :
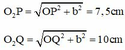
Tại Q là phần tử nước dao động với biên độ cực đại nên : ![]()
Tại P là phần tử nước không dao động nên P thuộc cực tiểu bậc k’
![]()
![]()
với k’ = k + 1 (do giữa P và Q không còn cực đại nào)
![]()
![]()
Q là cực đại ứng với k = 1 nên cực đại M gần P nhất ứng với k = 2
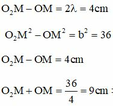
![]() hay OM = 2,5 cm
hay OM = 2,5 cm
Do đó : MP = 5,5 – 2,5 = 2 cm.

Đáp án B
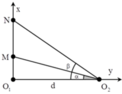
+ Ta có tan α = a d tan β = b d với d = O 1 O 2 = 18 c m .
tan M O 2 N ^ = tan β - α = tan β - tan α 1 + tan β tan α = a d - b d 1 + a d b d = d a - b d 2 + a b
+ Kết hợp a b = 324 ⇒ a = 324 b .
→ tan M O 2 N ^ = tan β - α = 1 36 b - 324 b = f b .
+ Ta có f ' b = 1 36 1 + 324 b 2 > 0 ∀ b trong 21 , 6 ; 24
→ M O 2 N ^ cực đại khi b=24cm, O 2 N = 30 c m O 2 M = 22 , 5 c m
+ M và N là hai cực đại ứng với bậc k và k+2, ta có:
O 2 M - a = k + 2 λ O 2 N - b = k λ ⇔ 22 , 5 - 13 , 5 = k + 2 λ 30 - 24 = k λ ⇒ λ = 1 , 5 c m .
Số cực đại giao thoa trên O 1 O 2 :
- O 1 O 2 λ ≤ k ≤ O 1 O 2 λ ⇔ - 18 1 , 5 ≤ k ≤ 18 1 , 5 ⇔ - 12 ≤ k ≤ 12 -> Có 25 điểm

Đáp án B
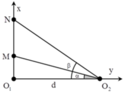
+ Ta có tan α = a d tan β = b d với d = O 1 O 2 = 18 c m .
tan M O 2 N ^ = tan β - α = tan β - tan α 1 + tan β tan α = a d - b d 1 + a d b d = d a - b d 2 + a b
Kết hợp a b = 324 ⇒ a = 324 b .
→ tan M O 2 N ^ = tan β - α = 1 36 b - 324 b = f b .
+ Ta có f ' b = 1 36 1 + 324 b 2 > 0 ∀ b trong 21 , 6 ; 24
→ M O 2 N ^ cực đại khi b=24cm. → a = 13 , 5 c m , O 2 N = 30 c m , O 2 M = 22 , 5 c m
+ M và N là hai cực đại ứng với bậc k và k+2, ta có:
O 2 M - a = k + 2 λ O 2 N - b = k λ ⇔ 22 , 5 - 13 , 5 = k + 2 λ 30 - 24 = k λ ⇒ λ = 1 , 5 c m .
Số cực đại giao thoa trên O 1 O 2 :
- O 1 O 2 λ ≤ k ≤ O 1 O 2 λ ⇔ - 18 1 , 5 ≤ k ≤ 18 1 , 5 ⇔ - 12 ≤ k ≤ 12
-> có 25 điểm

Có tan P O 2 Q = tan α - β = tan α - tan β 1 + tan α . tan β = 8 a - 4 ٫ 5 a 1 + 8 a . 4 ٫ 5 a = 3 ٫ 5 a + 36 a
Áp dụng BĐT Cauchy cho mẫu, ta tìm được
tan P O 2 Q ≤ 3 ٫ 5 12 ⇒ P O 2 Q m a x ⇔ a = 6 c m .
Q là cực đại, P là cực tiểu gần nguồn hơn và gần Q nhất nên ta có :
Q O 2 - Q O 1 = k λ P O 2 - P O 1 = k + 0 ٫ 5 λ ⇔ k λ = 2 k + 0 ٫ 5 λ = 3 ⇔ λ = 2 c m k = 1
Gọi M là cực đại gần P nhất. Vì Q là cực đại với k = 1 nên M là cực đại với k = 2.
⇒ M O 2 - M O 1 = 2 λ = 4 ⇒ M O 1 2 + 36 - M O 1 = 4 ⇔ M O 1 = 2 ٫ 5 c m
Suy ra PM = 4,5 – 2,5 = 2 (cm).