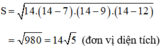Số đo của 3 cạnh tam giác lần lượt: \(\sqrt{13};\sqrt{17};2.\sqrt{5}\)Tìm diện tích tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài các cạnh lần lượt là a; b; c ( a; b; c khác 0 )
Ta có : \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)và a + b + c = 40,5
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{3}=2,7\Rightarrow a=8,1\\\frac{b}{5}=2,7\Rightarrow b=13,5\\\frac{c}{7}=2,7\Rightarrow c=18,9\end{cases}}\)
Vậy,........
gọi 3 cạch của tam giác lần lượt là a,b,c tương ứng với tỉ lệ 3,5,7 .
Theo đề bài ta có : a+b+c=40,5
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b+c}{3+5+7}=\frac{40,5}{15}=2,7\)
a/3=2,7 => a=2,7.3=8,1
b/5=2,7 => b=2,7.5=13,5
c/7=2,7 => c=2,7.7=18,9
Vậy 3 cạnh của tam giác có số đo lần lượt là 8,1cm ; 13,5cm ; 18,9cm

Gọi độ dài các cạnh MN, NP, MP lần lượt là \(a,b,c\left(cm\right);a,b,c>0\).
Vì độ dài các cạnh MN, NP, MP lần lượt tỉ lệ với \(3,4,5\)nên \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\).
Vì chu vi tam giác MNP là \(60cm\)nên \(a+b+c=60\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5\)
\(\Leftrightarrow\hept{\begin{cases}a=5.3=15\\b=5.4=20\\c=5.5=25\end{cases}}\)

+Dùng thước thẳng vẽ AB daì 3 cm
+Dùng compa vẽ cung tròn tâm A bán kính 4 cm
+Dùng compa vẽ cung tròn tâm B bán kính 5 cm
+Giao điểm 2 cung tròn chính là C
+Nối chúng lại và ta được tam giác ABC

Nửa chu vi của tam giác: p = (7 + 9 + 12)/2 = 14.
Áp dụng công thức Hê–rông ta có: