Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nửa chu vi của tam giác: p = (7 + 9 + 12)/2 = 14.
Áp dụng công thức Hê–rông ta có:
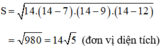

Ta có 2p = 7 + 9 + 12 => p = 14
p – a = 14 – 7 = 7
p – b = 14 – 9 = 5
p – c = 12 – 12 = 2
Áp dụng công thức Hê ron:
S = =
= 14√5 (dvdt)

S2= p(p-AB)(p-AC)(p-BC) *
mà p=(a+b+c):2
=> p= (7+9+12):2
=> p= 14 (đvđđd)
*<=> S2=14(14-7)(14-9)(14-12)
<=>S=\(\sqrt{\left(980\right)}\)
<=> S=\(14\sqrt{5}\)
S= (abc):4R => S=(7x9x12):4R => S=756:4R
=> R=6
S=pr
=> S=14r
=> r= \(\sqrt{\left(5\right)}\)

Tham khảo:
a) Đặt \(a = BC,b = AC,c = AB.\)
Ta có: \(p = \frac{1}{2}(15 + 18 + 27) = 30\)
Áp dụng công thức heron, ta có:
\({S_{ABC}} = \sqrt {30(30 - 15)(30 - 18)(30 - 27)} = 90\sqrt 2 \)
Và \(r = \frac{S}{p} = \frac{{90\sqrt 2 }}{{30}} = 3\sqrt 2 \)
b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.
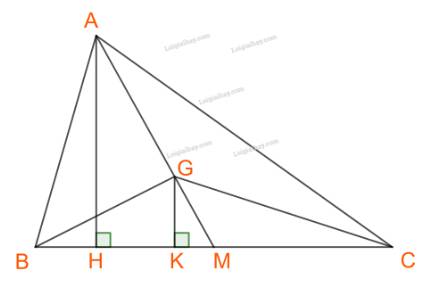
G là trọng tâm tam giác ABC nên \(GM = \frac{1}{3}AM\)
\(\begin{array}{l} \Rightarrow GK = \frac{1}{3}.AH\\ \Rightarrow {S_{GBC}} = \frac{1}{3}.\,{S_{ABC}} = \frac{1}{3}.90\sqrt 2 = 30\sqrt 2 .\end{array}\)

Tham khảo:
Kí hiệu các điểm A, B, C như hình dưới

Đặt \(AB = c,AC = b,BC = a.\)
Ta có: \(BC = 3,2;\widehat A = {180^o} - ({48^o} + {105^o}) = {27^o}\)
Áp dụng định lí sin, ta có:
\(\frac{b}{{\sin B}} = \frac{a}{{\sin A}} \Rightarrow AC = b = \frac{{a.\sin B}}{{\sin A}} = \frac{{3,2.\sin {{48}^o}}}{{\sin {{27}^o}}} \approx 5,24(m)\)
Áp dụng công thức \(S = \frac{1}{2}ab\sin C\) ta có:
\(S = \frac{1}{2}.3,2.5,24\sin {105^o} \approx 8,1({m^2})\)

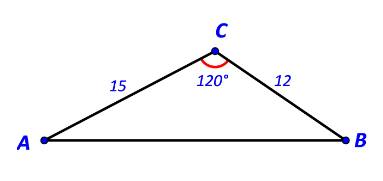
a) Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} - 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}\)
b) Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44\)
\( \Rightarrow \widehat A \approx {26^o}\) hoặc \(\widehat A \approx {154^o}\) (Loại)
Khi đó: \(\widehat B = {180^o} - ({26^o} + {120^o}) = {34^o}\)
c)
Diện tích tam giác ABC là: \(S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3 \)

Từ định lí cosin trong tam giác ABC, ta suy ra: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)
Mà \({\sin ^2}A + {\cos ^2}A = 1\)
\( \Rightarrow \sin A = \pm \sqrt {1 - {{\cos }^2}A} \)
Do \({0^o} < \widehat A < {180^o}\) nên \(\sin A > 0\) hay \(\sin A = \sqrt {1 - {{\cos }^2}A} \)
Ta có:
\(\begin{array}{l}\sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}} = \sqrt {1 - \frac{{{{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} \\ = \sqrt {\frac{{4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} = \frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}}\end{array}\)
Thế vào công thức tính diện tích tam giác ABC ta được:
\(S = \frac{1}{2}bc.\frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}} = \frac{1}{4}.\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} \)
Chú ý:
Nếu tiếp tục biến đổi công thức diện tích ta được
\(\begin{array}{l}S = \frac{1}{4}.\sqrt {\left( {2bc + {b^2} + {c^2} - {a^2}} \right)\left( {2bc - {b^2} - {c^2} + {a^2}} \right)} \\ = \frac{1}{4}.\sqrt {\left[ {{{\left( {b + c} \right)}^2} - {a^2}} \right]\left[ {{a^2} - {{\left( {b - c} \right)}^2}} \right]} \\ = \frac{1}{4}.\sqrt {\left( {b + c - a} \right)\left( {b + c + a} \right)\left( {a - b + c} \right)\left( {a + b - c} \right)} \end{array}\)
Đến đây, đặt \(p = \frac{{a + b + c}}{2}\), là nửa chu vi tam giác ABC, ta suy ra:
\(\left\{ \begin{array}{l}b + c + a = 2p\\b + c - a = b + c + a - 2a = 2\left( {p - a} \right)\\a - b + c = b + c + a - 2b = 2\left( {p - b} \right)\\a + b - c = b + c + a - 2c = 2\left( {p - c} \right)\end{array} \right.\)
\(\begin{array}{l} \Rightarrow S = \frac{1}{4}\sqrt {2\left( {p - a} \right).2p.2\left( {p - b} \right).2\left( {p - c} \right)} \\ \Leftrightarrow S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \end{array}\)
(công thức Heron)

Chọn D.
Diện tích tam giác ABC ban đầu là
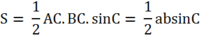
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là
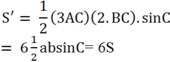

Ta có 2p = 7 + 9 + 12 => p = 14
p - a = 14 - 7 = 7
p - b = 14 - 9 = 5
p - c = 12 - 12 = 2
Áp dụng công thức Hê ron:
S =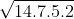 =
= 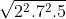 = 14√5 (dvdt)
= 14√5 (dvdt)