Bài 2. Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC.
a) Chứng minh ΔAHB = ΔAHC.
b) Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng ΔADE cân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*) Ta có: ΔABC cân tại A

BD = CE (giả thiết)
Suy ra: ΔABD = ΔACE (c.g.c)
⇒ AD = AE ( hai cạnh tương ứng)
*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó; ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
b: Ta có: ΔABH=ΔACK
nên \(\widehat{ABH}=\widehat{ACK}\)
c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)
\(\widehat{OCB}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{KCE}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O

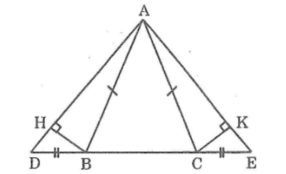
Vì ΔABC cân tại A nên∠(ABC) =∠(ACB) (tính chất tam giác cân)
Ta có: ∠(ABC) +∠(ABD) =180o(hai góc kề bù)
∠(ACB) +∠(ACE) =180o(hai góc kề bù)
Suy ra: ∠(ABD) =∠(ACE)
Xét ΔABD và ΔACE, ta có:
AB = AC (gt)
∠(ABD) =∠(ACE) (chứng minh trên)
BD=CE (gt)
Suy ra: ΔABD= ΔACE (c.g.c)
⇒∠D =∠E (hai góc tương ứng)
Xét hai tam giác vuông ΔBHD và ΔCKE, ta có:
∠(BHD) =∠(CKE) = 90º
BD=CE (gt)
∠D =∠E (chứng minh trên)
Suy ra: ΔBHD= ΔCKE (cạnh huyền – góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)

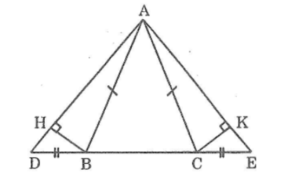
Xét ΔABH và ΔACK, ta có:
AB = AC (gt)
∠(AHB) =∠(AKC) =90o
BH=CK ( chứng minh trên)
Suy ra: ΔABH= ΔACK (cạnh huyền– cạnh góc vuông)

tự vẽ hình
a) Xét ΔADE có :
HE là đường trung tuyến của AD HA=HD )(1)
Ta thấy HC=12BC ( AH là đường trung tuyến của BC )
Mà BC = CE (gt )
⇒HC=12CE (2)
Từ (1) và (2) ⇒C là trọng tâm của ΔADE
b) Hơi khó đấy :)
Xét ΔAHB và ΔAHC có :
HAHA chung
HB=HC ( AH là đường trung tuyến của BC )
AB=AC( ΔABC cân tại A )
Do đó : ΔAHB=ΔAHC(c−c−c)
⇒AHBˆ=AHCˆ( hai góc tương ứng )
Mà AHBˆ+AHCˆ=1800
⇒AHB^=AHC^=1800/2=90o
Xét ΔAHEvà ΔHED có :
HEHE chung
HA=HD( HE là đường trung tuyến của AD )
AHEˆ=DHEˆ(=900)
Do đó : ΔAHE=ΔDHE ( hai cạnh góc vuông )
⇒AEHˆ=DEHˆ ( góc tương ứng ) (*)
Vì C là trọng tâm của ΔAED là đường trung tuyến của DE )
Xét vuông tại H có : HM là đường trung tuyến nối từ đỉnh H đến DE
⇒HM=DM (1)
Lưu ý : Trong tam giác vuông , đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền . Tức HM=12DE Mà 12DE=DM⇒HM=DM
Trở lại vào bài :
Mặt khác DM=ME(cmt)(2)
Từ (1) và (2) ⇒HM=ME
⇒ΔHME⇒ΔHME cân tại M
⇒MHEˆ=MEHˆ
Dễ thấy MEHˆ=HEAˆ(cmt)
⇒MHEˆ=HEAˆ
mà hai góc này ở vị trí so le trong
⇒HM⇒HM//AE(đpcm)

a: Xét ΔABM và ΔACN có
AB=AC
góc ABM=góc ACN
BM=CN
=>ΔABM=ΔACN
=>AM=AN
b: góc MBD=góc ECN
=>góc KBC=góc KCB
=>K nằm trên trung trực của BC
=>A,H,K thẳng hàng

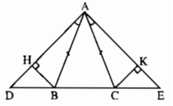
+) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)
Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)
∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)
Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE
+) Xét ΔABD và ΔACE có:
∠DAB = ∠EAC ( giả thiết)
AB = AC (vì tam giác ABC cân tại A)
∠ABD = ∠ACE ( chứng minh trên )
⇒ ΔABD = ΔACE (g.c.g)
⇒ BD = CE ( hai cạnh tương ứng)..
Lời giải:
a) Xét tam giác $AHB$ và $AHC$ có:
$AH$ chung
$AB=AC$ do $ABC$ cân tại $A$
$\widehat{AHB}=\widehat{AHC}=90^0$
$\Rightarrow \triangle AHB=\triangle AHC$ (ch-cgv)
b)
Vì $ABC$ cân tại $A$ nên $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABD}=\widehat{ACE}$
Xét tam giác $ABD$ và $ACE$ có:
$BD=CE$
$AB=AC$
$\widehat{ABD}=\widehat{ACE}$ (cmt)
$\Rightarrow \triangle ABD=\triangle ACE$ (c.g.c)
$\Rightarrow AD=AE$ nên $ADE$ là tam giác cân.
Hình vẽ: